15 Out Of 16 As A Percentage
Webtuts
May 09, 2025 · 4 min read
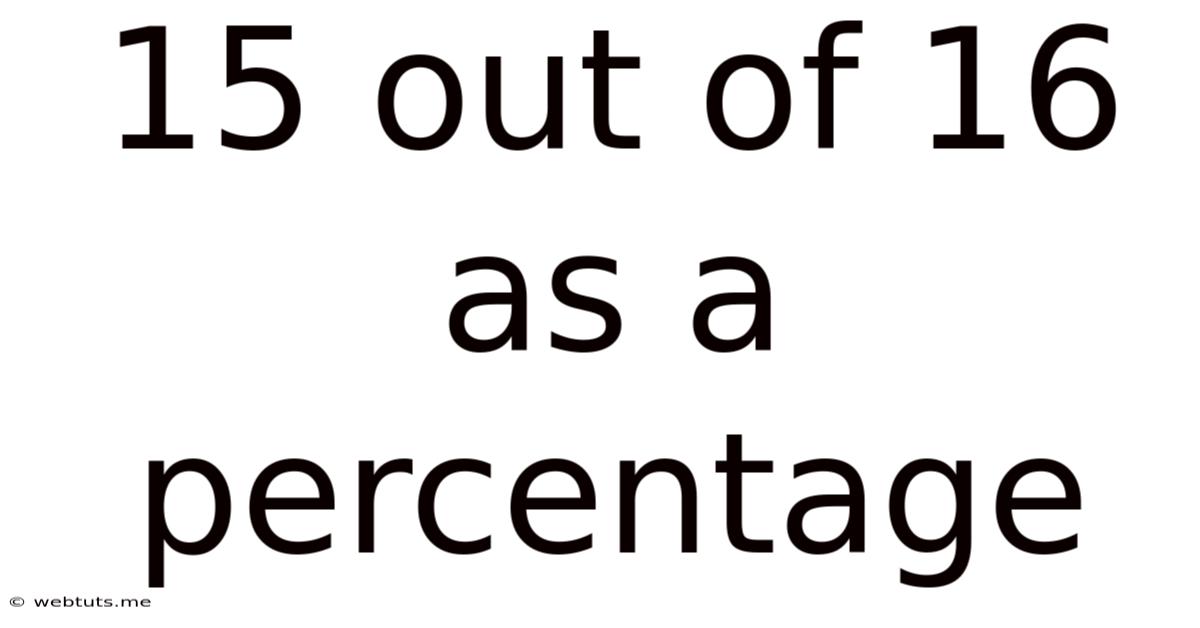
Table of Contents
15 out of 16 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill in various aspects of life, from academic studies to professional settings. Understanding how to express fractions as percentages is crucial for interpreting data, making comparisons, and presenting information effectively. This comprehensive guide will delve into the calculation of "15 out of 16 as a percentage," exploring different methods, applications, and related concepts. We'll also examine the broader context of percentage calculations and their importance in various fields.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol used to represent a percentage is "%". Essentially, it shows the proportional relationship of a part to a whole, where the whole is considered to be 100 units. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Understanding percentages is vital for many everyday tasks:
- Financial Calculations: Interest rates, discounts, tax calculations, and profit margins are all expressed as percentages.
- Data Analysis: Percentages are used to represent proportions in charts, graphs, and statistical reports, making it easy to visualize and interpret data.
- Academic Assessments: Grades, test scores, and performance metrics are often expressed as percentages.
- Everyday Life: Sales discounts, tip calculations, and recipe adjustments all involve percentage calculations.
Calculating 15 out of 16 as a Percentage: Three Methods
There are several ways to calculate 15 out of 16 as a percentage. Let's explore three common methods:
Method 1: Using the Fraction Method
This is the most straightforward approach. We represent "15 out of 16" as a fraction: 15/16. To convert this fraction to a percentage, we multiply it by 100%:
(15/16) * 100% = 93.75%
Therefore, 15 out of 16 is 93.75%.
Method 2: Using Decimal Conversion
First, we convert the fraction 15/16 into a decimal by dividing 15 by 16:
15 ÷ 16 = 0.9375
Then, we multiply the decimal by 100% to express it as a percentage:
0.9375 * 100% = 93.75%
Again, we arrive at the same result: 93.75%.
Method 3: Using Proportions
This method involves setting up a proportion to solve for the unknown percentage:
15/16 = x/100
To solve for 'x', we cross-multiply:
16x = 1500
x = 1500/16
x = 93.75
Therefore, x = 93.75%.
Real-World Applications of 93.75%
The percentage 93.75% has numerous applications across diverse fields. Consider these examples:
- Academic Performance: A student scoring 15 out of 16 on a test achieved a grade of 93.75%. This highlights a high level of understanding and mastery of the subject matter.
- Manufacturing Quality Control: In a production run of 16 items, if 15 meet quality standards, the quality control rate is 93.75%. This indicates a high level of efficiency and precision in the manufacturing process.
- Survey Results: If 15 out of 16 respondents answered "yes" to a particular question in a survey, the positive response rate is 93.75%. This indicates a strong consensus or preference.
- Project Completion: If 15 out of 16 tasks in a project are completed, the project completion rate is 93.75%. This signifies significant progress towards project goals.
Beyond 15 out of 16: Mastering Percentage Calculations
Understanding how to calculate 15 out of 16 as a percentage provides a foundation for tackling other percentage problems. Here are some key concepts to enhance your skills:
- Converting Fractions to Percentages: The general formula is (Fraction) * 100% = Percentage.
- Converting Decimals to Percentages: The general formula is (Decimal) * 100% = Percentage.
- Converting Percentages to Fractions: Divide the percentage by 100 and simplify the resulting fraction.
- Calculating Percentage Increase/Decrease: This involves finding the difference between two values, dividing by the original value, and multiplying by 100%.
- Finding a Percentage of a Number: Multiply the number by the percentage (expressed as a decimal).
Tips for Accurate Percentage Calculations
- Double-check your calculations: Always verify your work to avoid errors.
- Use a calculator: Calculators can be helpful for complex calculations.
- Understand the context: Make sure you understand the meaning of the numbers and the question being asked.
- Practice regularly: The more you practice, the better you'll become at calculating percentages.
Conclusion: The Significance of Percentage Calculations
The ability to calculate percentages is a valuable skill with far-reaching applications. Understanding the different methods for calculating percentages, such as the fraction method, decimal conversion, and proportions, allows for flexibility and accuracy. Mastering percentage calculations is essential for success in academics, professional life, and navigating everyday situations requiring proportional reasoning. The example of 15 out of 16 as a percentage, equaling 93.75%, illustrates the importance of this skill in interpreting data and understanding proportions accurately. By continuing to practice and refine your skills, you will enhance your ability to analyze data, make informed decisions, and communicate effectively using this fundamental mathematical tool. Remember, accuracy and understanding are key to mastering percentage calculations.
Latest Posts
Latest Posts
-
83 Kilograms Is How Many Pounds
May 11, 2025
-
How Much Is 90g Of Butter
May 11, 2025
-
6 Cups Equals How Many Pints
May 11, 2025
-
What Is 500 Seconds In Minutes
May 11, 2025
-
120 Days From June 21 2024
May 11, 2025
Related Post
Thank you for visiting our website which covers about 15 Out Of 16 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.