8 Out Of 9 As A Percent
Webtuts
May 13, 2025 · 4 min read
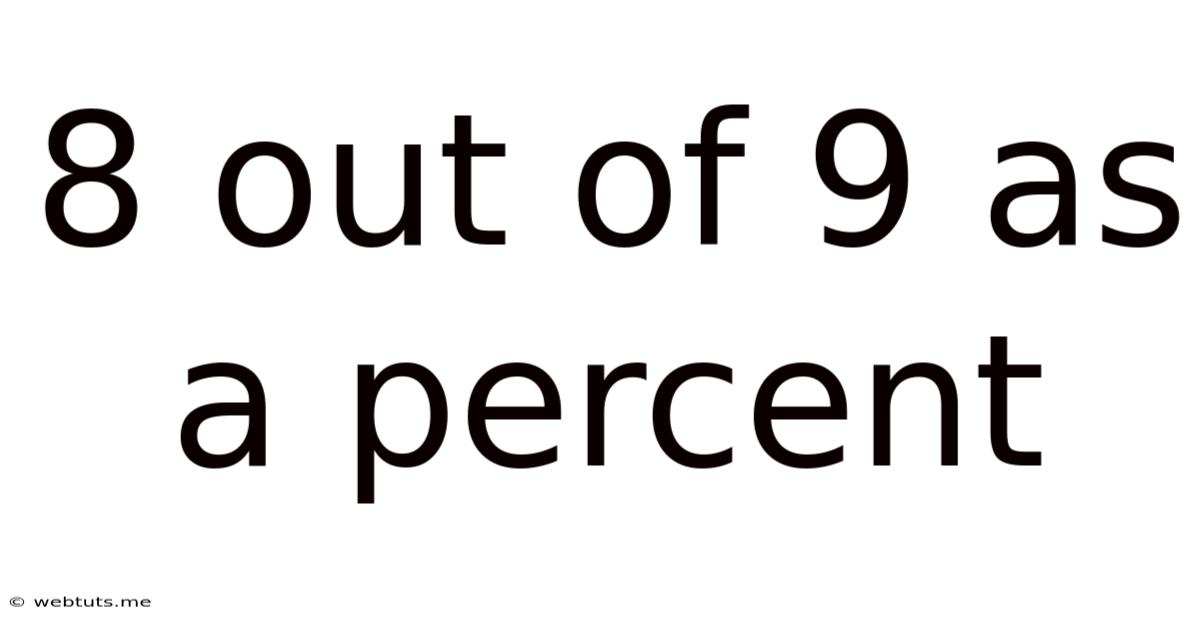
Table of Contents
8 Out of 9 as a Percent: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analyses. This comprehensive guide will delve into calculating "8 out of 9 as a percent," explaining the process, exploring variations, and providing practical applications. We'll also touch upon related concepts to solidify your understanding of percentages.
Understanding the Fundamentals of Percentages
Before we tackle the specific problem of converting "8 out of 9" into a percentage, let's review the basic principles. A percentage represents a fraction of 100. The word "percent" itself originates from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be expressed as a fraction with a denominator of 100.
Key Concepts:
- Fraction: A fraction represents a part of a whole. In our case, "8 out of 9" is a fraction, where 8 is the numerator (the part) and 9 is the denominator (the whole).
- Decimal: Decimals are another way to represent fractions, where the decimal point separates the whole number from the fractional part.
- Percentage: The percentage is the equivalent of the fraction or decimal expressed as a portion of 100.
Calculating 8 Out of 9 as a Percentage: Step-by-Step Guide
To convert the fraction 8/9 into a percentage, we need to follow these simple steps:
Step 1: Convert the Fraction to a Decimal
Divide the numerator (8) by the denominator (9):
8 ÷ 9 = 0.888...
Note that this decimal is recurring, meaning the digit 8 repeats infinitely. For practical purposes, we'll round this to a suitable number of decimal places.
Step 2: Convert the Decimal to a Percentage
Multiply the decimal by 100:
0.888... × 100 ≈ 88.89%
We round the result to two decimal places for precision.
Therefore, 8 out of 9 is approximately 88.89%.
Practical Applications and Real-World Examples
Understanding how to calculate percentages is crucial in various real-world scenarios. Here are some examples where this skill comes in handy:
- Academic Performance: Imagine a student who answered 8 out of 9 questions correctly on a test. Calculating the percentage score (88.89%) gives a clear picture of their performance.
- Sales and Discounts: Businesses often advertise discounts as percentages. For example, a "10% off" sale means you'll pay 90% of the original price. Being able to calculate these percentages helps consumers make informed decisions.
- Financial Calculations: Calculating interest rates, taxes, and investment returns all involve percentages. Understanding these calculations is essential for effective financial planning.
- Statistical Analysis: Percentages are frequently used in data analysis and statistics to represent proportions and trends. For example, representing survey results or market share often involves converting data into percentages.
- Cooking and Baking: Recipes often use percentages to indicate the proportion of ingredients. For instance, a recipe might call for 80% flour and 20% water.
Variations and Related Percentage Calculations
While we've focused on 8 out of 9, understanding how to calculate percentages allows you to tackle other similar problems. Let's explore some variations:
1. Calculating a Percentage of a Number:
If you need to calculate 88.89% of a larger number, say, 150, you multiply 150 by 0.8889 (the decimal equivalent of 88.89%):
150 × 0.8889 ≈ 133.335
2. Finding the Original Amount:
If you know a percentage and the resulting amount, you can work backward to find the original number. For example, if 88.89% of a number is 133.335, divide 133.335 by 0.8889:
133.335 ÷ 0.8889 ≈ 150
3. Calculating Percentage Increase or Decrease:
These calculations involve comparing two values and expressing the difference as a percentage. For instance, if a value increases from 100 to 120, the percentage increase is:
[(120 - 100) / 100] × 100% = 20%
4. Dealing with Complex Fractions:
Sometimes you might encounter more complex fractions. The principle remains the same: convert the fraction to a decimal and then to a percentage.
Advanced Concepts and Further Exploration
For a deeper understanding of percentages and their applications, you can explore more advanced concepts such as:
- Compound interest: This involves calculating interest on both the principal and accumulated interest.
- Percentage points: This refers to the absolute difference between two percentages, not the relative change.
- Weighted averages: This method considers the relative importance of different data points when calculating an average.
- Statistical significance testing: In statistics, percentages play a critical role in determining the significance of research findings.
Conclusion: Mastering Percentage Calculations for Success
Mastering percentage calculations is an invaluable skill with widespread applications in daily life and professional settings. By understanding the fundamental principles, practicing various scenarios, and exploring more advanced concepts, you'll equip yourself with a powerful tool for navigating a world filled with numerical data. Remember that accuracy is crucial, and employing appropriate rounding techniques ensures your calculations remain reliable and meaningful. The ability to confidently convert fractions like "8 out of 9" into percentages will significantly enhance your problem-solving skills and analytical capabilities. So keep practicing, and soon you'll be a percentage pro!
Latest Posts
Latest Posts
-
Miles Per Hour To Meters Per Hour
May 14, 2025
-
How Long Till Summer In Months
May 14, 2025
-
400 Sq In To Sq Ft
May 14, 2025
-
How Many More Hours Until 6
May 14, 2025
-
How To Calculate A Yard Of Soil
May 14, 2025
Related Post
Thank you for visiting our website which covers about 8 Out Of 9 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.