What Is 0.375 As A Fraction
Webtuts
May 14, 2025 · 5 min read
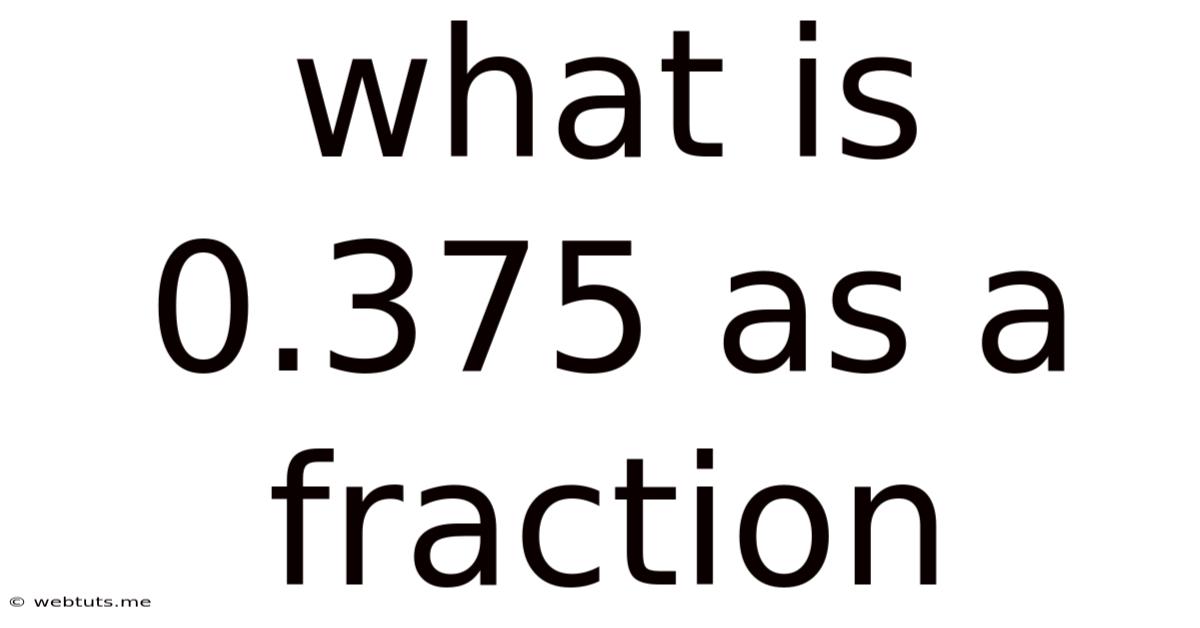
Table of Contents
What is 0.375 as a Fraction? A Comprehensive Guide
Understanding decimal-to-fraction conversions is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert the decimal 0.375 into a fraction but also delve into the underlying principles, providing you with the tools to tackle similar conversions with confidence. We'll explore different methods, address common misconceptions, and offer practical applications to solidify your understanding.
Understanding Decimals and Fractions
Before we dive into the conversion, let's refresh our understanding of decimals and fractions.
-
Decimals: Decimals represent numbers that are not whole numbers. They use a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
-
Fractions: Fractions represent a part of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, and the denominator indicates the total number of equal parts the whole is divided into.
Method 1: Using the Place Value Method
This is perhaps the most straightforward method for converting terminating decimals (decimals that end) into fractions.
-
Identify the place value of the last digit: In 0.375, the last digit (5) is in the thousandths place. This means the denominator of our fraction will be 1000.
-
Write the decimal as a fraction: Write the digits to the right of the decimal point as the numerator, and the place value as the denominator. This gives us: 375/1000
-
Simplify the fraction: Now, we need to simplify the fraction to its lowest terms. This means finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD of 375 and 1000 is 125.
375 ÷ 125 = 3 1000 ÷ 125 = 8
Therefore, the simplified fraction is 3/8.
Method 2: Using Equivalent Fractions
This method involves understanding that multiplying or dividing both the numerator and denominator of a fraction by the same number doesn't change its value. We can use this principle to convert decimals to fractions.
-
Write the decimal as a fraction with a power of 10 as the denominator: We can write 0.375 as 375/1000 (as we did in Method 1).
-
Find common factors: Look for common factors between the numerator and denominator. Both 375 and 1000 are divisible by 5, 25, and 125.
-
Simplify by dividing: Divide both the numerator and the denominator by their greatest common divisor (125 in this case):
375 ÷ 125 = 3 1000 ÷ 125 = 8
Again, we arrive at the simplified fraction: 3/8.
Method 3: Using the Repeated Division Method (for recurring decimals)
While 0.375 is a terminating decimal, this method is useful for recurring decimals (decimals that repeat infinitely). It involves repeatedly dividing the decimal by powers of 10 until a whole number is obtained. Since 0.375 is not a recurring decimal, this method is not directly applicable here. However, let's illustrate with a recurring decimal example: 0.333... (one-third).
- Let x = 0.333...
- Multiply by 10: 10x = 3.333...
- Subtract the original equation: 10x - x = 3.333... - 0.333... This simplifies to 9x = 3
- Solve for x: x = 3/9 = 1/3
This demonstrates the principle, although it's not needed for 0.375.
Checking Your Answer: Converting the Fraction Back to a Decimal
To verify that 3/8 is indeed equal to 0.375, we can perform the reverse operation: divide the numerator (3) by the denominator (8).
3 ÷ 8 = 0.375
This confirms our conversion is correct.
Common Mistakes to Avoid
-
Forgetting to simplify: Always simplify your fraction to its lowest terms. A fraction like 375/1000 is correct, but 3/8 is the preferred and more concise representation.
-
Incorrect place value identification: Make sure you correctly identify the place value of the last digit in the decimal. A mistake here will lead to an incorrect fraction.
-
Dividing by the wrong number: When simplifying, make sure you divide both the numerator and the denominator by the same number (their greatest common divisor).
Practical Applications
Understanding decimal-to-fraction conversions is crucial in various contexts:
-
Baking and Cooking: Many recipes use fractions for ingredient measurements. Converting decimal amounts from a digital scale to fractional measurements is useful.
-
Engineering and Construction: Precision is paramount in these fields. Converting decimals to fractions ensures accuracy in calculations and measurements.
-
Finance: Dealing with percentages and proportions often involves working with fractions and decimals interchangeably.
-
Everyday calculations: Understanding how fractions and decimals relate helps in solving problems involving parts of a whole in daily life.
Further Exploration: Working with Mixed Numbers and Improper Fractions
-
Improper fractions: An improper fraction is one where the numerator is greater than or equal to the denominator (e.g., 5/4). While our example resulted in a proper fraction (3/8), understanding improper fractions is important for more complex conversions.
-
Mixed numbers: A mixed number combines a whole number and a proper fraction (e.g., 1 1/4). If a decimal is greater than 1 (e.g., 1.375), the conversion will result in a mixed number. To convert 1.375 to a fraction, you'd first subtract the whole number (1), convert 0.375 to 3/8, and then add the whole number back: 1 3/8.
Conclusion: Mastering Decimal-to-Fraction Conversions
Converting decimals to fractions, even seemingly simple ones like 0.375, involves a systematic approach and a solid understanding of fundamental mathematical principles. By mastering these techniques and avoiding common pitfalls, you can confidently tackle a wide range of decimal-to-fraction conversions in various contexts, enhancing your mathematical skills and problem-solving abilities. Remember to always simplify your fractions to their lowest terms for the most accurate and efficient representation.
Latest Posts
Latest Posts
-
How Many Days Till Aug 20
May 14, 2025
-
How Many More Days Till April 7
May 14, 2025
-
How Many Days To March 10
May 14, 2025
-
2 3 Cup Convert To Tablespoons
May 14, 2025
-
How Many Ounces In A 5 Pound Bag Of Flour
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 0.375 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.