What Is 0.375 In A Fraction
Webtuts
May 12, 2025 · 4 min read
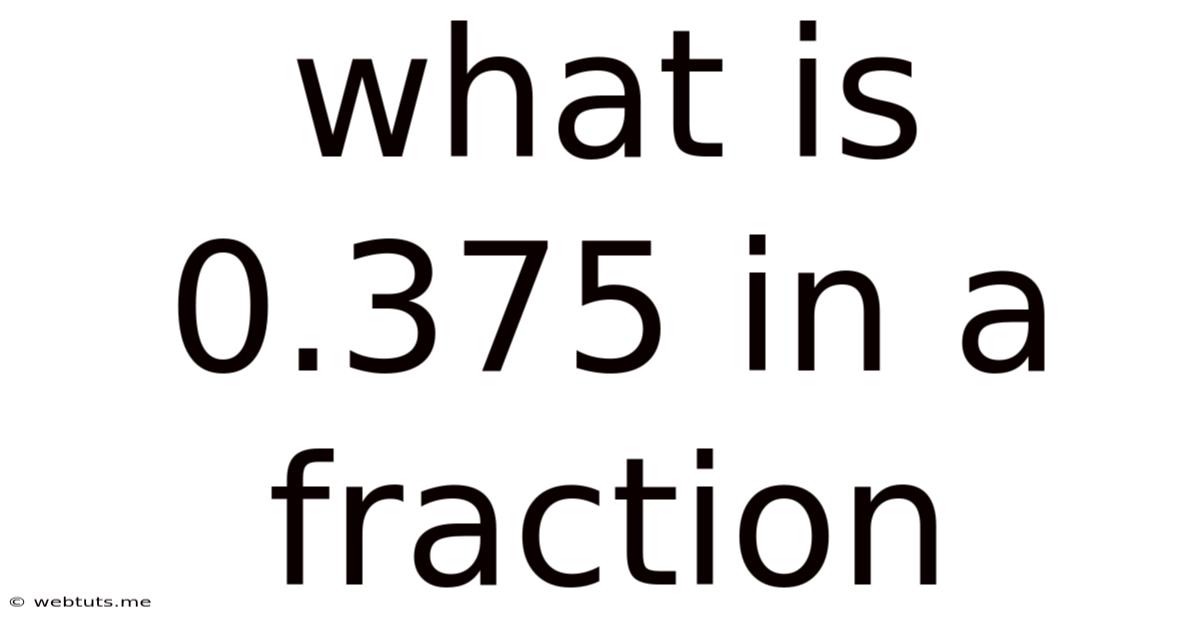
Table of Contents
What is 0.375 as a Fraction? A Comprehensive Guide
Converting decimals to fractions might seem daunting at first, but it's a fundamental skill with wide-ranging applications in mathematics, science, and everyday life. This comprehensive guide will walk you through the process of converting the decimal 0.375 into its fractional equivalent, explaining the method in detail and providing valuable insights into the broader concept of decimal-to-fraction conversion. We'll also explore practical applications and delve into related concepts to solidify your understanding.
Understanding Decimals and Fractions
Before diving into the conversion, let's refresh our understanding of decimals and fractions.
Decimals: Decimals represent numbers that are not whole numbers. They use a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent fractions with denominators that are powers of 10 (10, 100, 1000, and so on). For example, 0.375 represents three hundred seventy-five thousandths.
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts the whole is divided into. For instance, 3/4 means you have 3 parts out of a total of 4 parts.
Converting 0.375 to a Fraction: Step-by-Step
The key to converting a decimal to a fraction lies in recognizing the place value of the last digit. In 0.375, the last digit, 5, is in the thousandths place. This means the denominator of our fraction will be 1000.
Step 1: Write the decimal as a fraction with a denominator of 1000.
0.375 can be written as 375/1000.
Step 2: Simplify the fraction.
This step is crucial for representing the fraction in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of the numerator (375) and the denominator (1000). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Finding the GCD can be done using various methods, including prime factorization or the Euclidean algorithm. Let's use prime factorization for this example:
- Prime factorization of 375: 3 x 5 x 5 x 5 = 3 x 5³
- Prime factorization of 1000: 2 x 2 x 2 x 5 x 5 x 5 = 2³ x 5³
The common factors are 5³, which equals 125. Therefore, the GCD of 375 and 1000 is 125.
Step 3: Divide both the numerator and the denominator by the GCD.
Dividing both 375 and 1000 by 125, we get:
375 ÷ 125 = 3 1000 ÷ 125 = 8
Therefore, the simplified fraction is 3/8.
Verification: Converting the Fraction Back to a Decimal
To ensure our conversion is correct, let's convert the fraction 3/8 back to a decimal:
Divide the numerator (3) by the denominator (8): 3 ÷ 8 = 0.375
This confirms that our conversion is accurate. 0.375 is indeed equivalent to 3/8.
Practical Applications of Decimal-to-Fraction Conversion
The ability to convert decimals to fractions is invaluable in various contexts:
- Cooking and Baking: Recipes often require precise measurements. Converting decimal measurements to fractions ensures accuracy and consistency.
- Construction and Engineering: Precision is paramount in these fields. Converting decimal measurements to fractions helps in accurate calculations and avoiding errors.
- Finance: Working with percentages and proportions often requires converting decimals to fractions for easier calculations.
- Science and Engineering: Many scientific and engineering calculations involve fractions, making the conversion skill essential.
- Mathematics: Understanding decimal-to-fraction conversion is fundamental for mastering more advanced mathematical concepts.
Beyond 0.375: Generalizing the Conversion Process
The method used to convert 0.375 to a fraction applies to any terminating decimal (a decimal that ends). Here's a generalized approach:
-
Identify the place value of the last digit: This determines the denominator of the initial fraction. If the last digit is in the tenths place, the denominator is 10. If it's in the hundredths place, the denominator is 100, and so on.
-
Write the decimal as a fraction: The digits to the right of the decimal point form the numerator, and the determined denominator is placed below.
-
Simplify the fraction: Find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD to obtain the simplified fraction.
Dealing with Repeating Decimals
While the process above works for terminating decimals, repeating decimals (decimals with a pattern that repeats infinitely) require a slightly different approach. This involves using algebraic techniques to solve for the fractional equivalent. For example, converting 0.333... (0.3 repeating) to a fraction involves setting up an equation and solving for x.
Conclusion
Converting decimals to fractions is a valuable mathematical skill with wide-ranging practical applications. Understanding the process, from identifying place values to simplifying fractions, is crucial for accuracy and efficiency in various fields. This guide provided a step-by-step approach to converting 0.375 to its fractional equivalent (3/8) and explored the broader context of decimal-to-fraction conversion, including handling terminating and repeating decimals. Mastering this skill empowers you to tackle more complex mathematical problems and excel in fields requiring precise calculations. Remember to always simplify your fractions to their lowest terms for the most accurate representation.
Latest Posts
Latest Posts
-
1 1 8 On A Tape Measure
May 13, 2025
-
How Many Gallons Of Dirt In A Cubic Yard
May 13, 2025
-
What Is 1 67 M In Feet
May 13, 2025
-
90 Days From November 18 2024
May 13, 2025
-
How Many More Days Till July 23
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 0.375 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.