What Is 1 3/4 Plus 1 3/4
Webtuts
May 10, 2025 · 4 min read
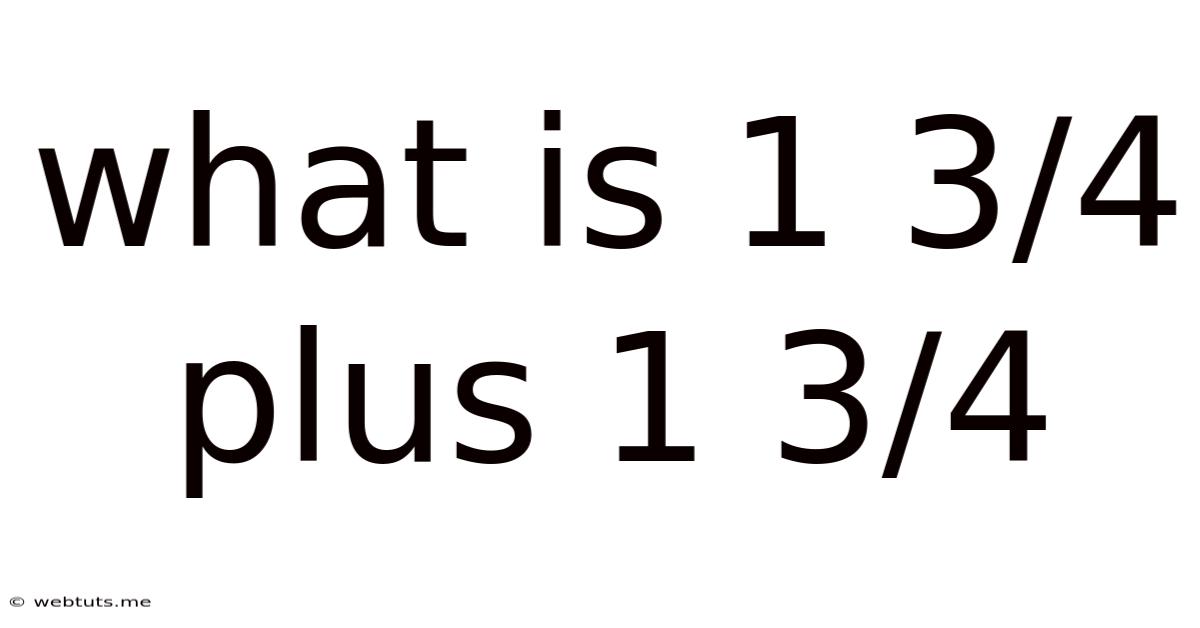
Table of Contents
What is 1 3/4 plus 1 3/4? A Deep Dive into Fraction Addition
Adding fractions might seem like a simple arithmetic task, but understanding the underlying principles is crucial for various applications, from baking to advanced mathematics. This comprehensive guide will delve into the seemingly straightforward problem of "What is 1 3/4 plus 1 3/4?" and explore the broader concepts of fraction addition, providing you with a solid foundation for future calculations. We'll also discuss different methods to solve this, highlighting the importance of understanding the 'why' behind the process.
Understanding Fractions: A Quick Recap
Before tackling the problem, let's revisit the basics of fractions. A fraction represents a part of a whole. It consists of two main parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, 3 is the numerator (we have 3 parts), and 4 is the denominator (the whole is divided into 4 equal parts).
Method 1: Converting Mixed Numbers to Improper Fractions
The given numbers, 1 3/4 and 1 3/4, are mixed numbers. A mixed number combines a whole number and a fraction. To add mixed numbers effectively, it's often easier to convert them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
Here's how to convert 1 3/4 to an improper fraction:
- Multiply the whole number by the denominator: 1 * 4 = 4
- Add the numerator to the result: 4 + 3 = 7
- Keep the same denominator: The improper fraction is 7/4.
Therefore, the problem "What is 1 3/4 plus 1 3/4?" becomes "What is 7/4 plus 7/4?".
Method 2: Adding the Whole Numbers and Fractions Separately
Another approach is to add the whole numbers and the fractions separately:
- Add the whole numbers: 1 + 1 = 2
- Add the fractions: 3/4 + 3/4 = 6/4
- Combine the results: 2 + 6/4 = 2 6/4
However, this result still contains an improper fraction (6/4). We need to simplify it.
Simplifying Improper Fractions
To simplify 6/4, we divide the numerator (6) by the denominator (4):
6 ÷ 4 = 1 with a remainder of 2.
This means 6/4 can be expressed as 1 2/4.
Therefore, the complete answer becomes 2 + 1 2/4 = 3 2/4.
Further Simplification: Reducing Fractions
Notice that 2/4 can be simplified further. Both the numerator and the denominator are divisible by 2:
2 ÷ 2 = 1 4 ÷ 2 = 2
So, 2/4 simplifies to 1/2.
Thus, the final, simplified answer is 3 1/2.
Method 3: Direct Addition of Improper Fractions
Using the improper fraction method from the beginning, we have 7/4 + 7/4. Since the denominators are the same, we can simply add the numerators:
7 + 7 = 14
So, the sum is 14/4. This is an improper fraction that needs simplification:
14 ÷ 4 = 3 with a remainder of 2.
Therefore, 14/4 = 3 2/4, which simplifies to 3 1/2.
Visual Representation: Understanding the Concept
Imagine two pizzas, each cut into four equal slices. If you take 3 slices from one pizza (1 3/4) and 3 slices from the other (1 3/4), you have a total of 6 slices. Since each pizza has 4 slices, you have 6/4 pizzas, which simplifies to 1 and 2/4 pizzas, or 1 1/2 pizzas. Adding this to the two whole pizzas you started with (one from each pizza) gives you a total of 3 1/2 pizzas.
Practical Applications of Fraction Addition
The ability to add fractions is essential in many real-world situations:
- Cooking and Baking: Recipes often require fractional measurements of ingredients.
- Construction and Engineering: Precise measurements are crucial in these fields.
- Finance: Calculating interest, proportions, and shares involves fractions.
- Science: Many scientific calculations utilize fractions and decimals.
Beyond the Basics: Adding Fractions with Different Denominators
The problem we addressed involved fractions with the same denominator (4). However, adding fractions with different denominators requires an extra step: finding a common denominator.
For example, let's add 1/2 and 1/3. The common denominator is 6 (the least common multiple of 2 and 3). We convert the fractions:
1/2 = 3/6 1/3 = 2/6
Now, we can add them: 3/6 + 2/6 = 5/6
Conclusion: Mastering Fraction Addition
Adding fractions, even seemingly simple problems like 1 3/4 plus 1 3/4, involves a systematic approach. Understanding the process of converting mixed numbers to improper fractions, simplifying improper fractions, and finding common denominators is crucial for mastering this fundamental mathematical skill. The ability to confidently handle fraction addition will benefit you in various academic and practical settings. By understanding the underlying concepts and practicing different methods, you can build a solid foundation in mathematics and confidently tackle more complex fraction problems in the future. Remember, the key is not just knowing the answer (which is 3 1/2), but understanding why the answer is what it is. This deep understanding will serve you well in all your future mathematical endeavors.
Latest Posts
Latest Posts
-
How Many Mm Is 13 16
May 11, 2025
-
How Much A Yard Of Concrete Weigh
May 11, 2025
-
How Many More Days Until November 8th 2024
May 11, 2025
-
How Many More Days Until August 31st
May 11, 2025
-
How Many Pints Equal 6 Cups
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 3/4 Plus 1 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.