What Is 1 Out Of 3 In Percentage
Webtuts
May 13, 2025 · 5 min read
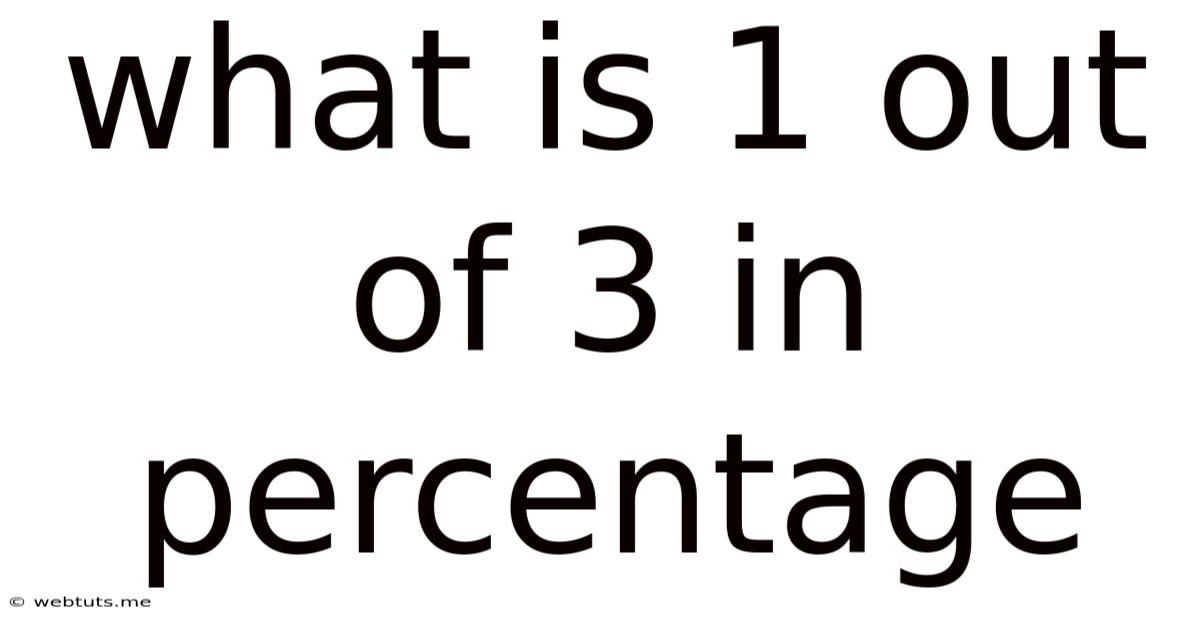
Table of Contents
What is 1 out of 3 in Percentage? A Comprehensive Guide
Knowing how to convert fractions to percentages is a fundamental skill with wide-ranging applications in various fields, from everyday calculations to complex statistical analysis. This comprehensive guide will delve into the specifics of determining what 1 out of 3 represents as a percentage, and will further explore the underlying principles and methods involved in fractional-to-percentage conversions. We'll also touch upon practical applications and provide you with the tools to confidently tackle similar problems in the future.
Understanding Fractions and Percentages
Before we jump into calculating the percentage, let's clarify the basics of fractions and percentages.
What is a Fraction?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into. In our case, 1 out of 3 can be written as the fraction 1/3.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" is used to denote a percentage. It essentially tells us what proportion of a whole is represented by a particular quantity, with 100% representing the entirety of the whole.
Calculating 1 out of 3 as a Percentage
To calculate what 1 out of 3 is as a percentage, we need to convert the fraction 1/3 into a percentage. Here's the step-by-step process:
Step 1: Convert the fraction to a decimal.
Divide the numerator (1) by the denominator (3):
1 ÷ 3 = 0.3333... (This is a recurring decimal)
Step 2: Multiply the decimal by 100.
This step converts the decimal to a percentage:
0.3333... × 100 = 33.333...%
Step 3: Round the percentage (optional).
Recurring decimals can be cumbersome. Depending on the level of precision required, you can round the percentage. Common rounding practices include rounding to one decimal place (33.3%), two decimal places (33.33%), or even to the nearest whole number (33%).
Therefore, 1 out of 3 is approximately 33.33%. The more decimal places you use, the more accurate your representation will be.
Different Methods for Conversion
While the above method is straightforward, let's explore other methods to achieve the same result. Understanding multiple approaches can deepen your understanding of the underlying concepts.
Using Proportions
We can also use proportions to solve this problem. We know that 1/3 represents a part of a whole, and we want to find what percentage this represents out of 100%. We can set up a proportion:
1/3 = x/100
To solve for x (the percentage), we cross-multiply:
3x = 100
x = 100/3 = 33.333...%
This method demonstrates the equivalence between the fraction and the percentage.
Using the Percentage Formula
The general percentage formula is:
Percentage = (Part/Whole) × 100%
In our case, the part is 1, and the whole is 3. Substituting these values into the formula gives:
Percentage = (1/3) × 100% = 33.333...%
Practical Applications of Percentage Calculations
Understanding how to convert fractions to percentages has numerous real-world applications. Here are a few examples:
- Sales and Discounts: If a store offers a 1/3 discount, you can quickly calculate that this is a 33.33% discount.
- Statistics and Probability: Many statistical analyses involve calculating percentages, such as the percentage of people who prefer a particular product or the probability of a certain event occurring.
- Finance: Calculating interest rates, returns on investments, and other financial metrics frequently involves working with percentages.
- Data Analysis: Representing data visually often requires converting fractions into percentages for charts and graphs.
- Everyday Life: From calculating tips in restaurants to understanding election results, percentage calculations are everywhere.
Beyond 1 out of 3: Extending the Concepts
The methods discussed above can be applied to any fraction. Let's consider a few examples to solidify your understanding:
- 2 out of 5: 2/5 = 0.4 × 100% = 40%
- 3 out of 4: 3/4 = 0.75 × 100% = 75%
- 5 out of 8: 5/8 = 0.625 × 100% = 62.5%
These examples illustrate how the same principles apply regardless of the specific fraction. The key steps remain consistent: convert the fraction to a decimal, then multiply by 100% to obtain the percentage.
Addressing Potential Challenges and Common Mistakes
While the process seems simple, some common mistakes can arise:
- Incorrect Order of Operations: Always divide the numerator by the denominator before multiplying by 100%.
- Rounding Errors: Be mindful of rounding and its impact on accuracy. Depending on the context, you may need to retain more decimal places for greater precision.
- Confusing Numerator and Denominator: Ensure you correctly identify the numerator (the part) and the denominator (the whole) in the fraction.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a vital skill across many disciplines. By understanding the underlying principles and utilizing the various methods discussed in this article, you can confidently tackle percentage calculations in any scenario. Remember to practice regularly, and you'll soon master this fundamental skill. The ability to accurately interpret and utilize percentages is invaluable in interpreting data, making informed decisions, and effectively communicating quantitative information. Through consistent practice and application, you can significantly improve your numeracy skills and enhance your ability to navigate the numerical aspects of everyday life and professional endeavors.
Latest Posts
Latest Posts
-
How Many Pounds Is 350 G
May 13, 2025
-
How Far Is 5000 Metres In Miles
May 13, 2025
-
How Many Weeks Are In 8 Years
May 13, 2025
-
90 Days From January 9 2024
May 13, 2025
-
6 Tbsp Is Equal To How Many Cups
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 Out Of 3 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.