What Is 7 Out Of 9 As A Percentage
Webtuts
May 14, 2025 · 5 min read
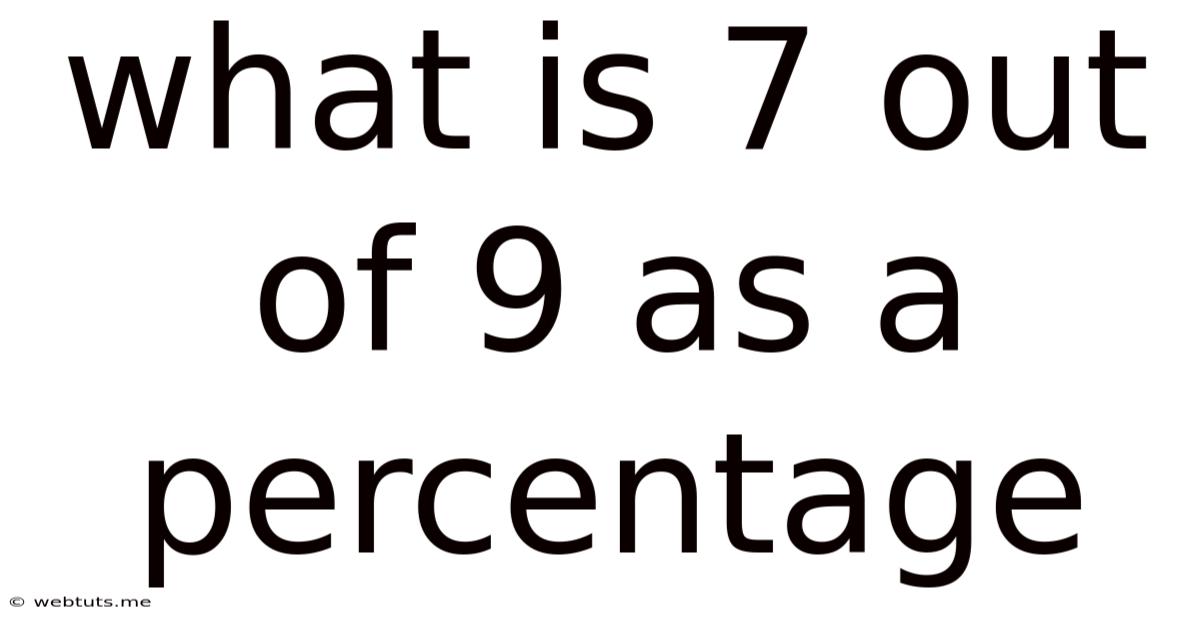
Table of Contents
What is 7 out of 9 as a Percentage? A Comprehensive Guide
Determining percentages is a fundamental skill applicable across numerous fields, from calculating grades to understanding financial statements and analyzing statistical data. This comprehensive guide will delve into how to calculate "7 out of 9 as a percentage," explaining the process step-by-step, providing alternative methods, and exploring its applications in various contexts. We'll also touch upon related concepts to solidify your understanding of percentage calculations.
Understanding Percentages
Before we tackle the specific problem, let's establish a firm grasp of percentages. A percentage represents a fraction of 100. The term "percent" itself originates from the Latin "per centum," meaning "out of one hundred." Therefore, any percentage can be expressed as a fraction with a denominator of 100. For instance, 50% is equivalent to 50/100, which simplifies to 1/2.
Calculating 7 out of 9 as a Percentage: The Primary Method
The most straightforward method involves converting the fraction "7 out of 9" into a percentage. Here's the step-by-step process:
1. Express as a Fraction: The phrase "7 out of 9" directly translates to the fraction 7/9.
2. Convert to a Decimal: To convert a fraction to a decimal, divide the numerator (7) by the denominator (9):
7 ÷ 9 = 0.777... (This is a recurring decimal)
3. Convert Decimal to Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.777... × 100 ≈ 77.78%
Therefore, 7 out of 9 is approximately 77.78%. The use of "approximately" is crucial here because the decimal is recurring; we've rounded it to two decimal places for practicality.
Alternative Methods for Calculating Percentages
While the primary method is efficient, alternative approaches can enhance understanding and provide flexibility depending on the context.
1. Using Proportions: A proportion establishes an equivalence between two ratios. We can set up a proportion to solve for the percentage:
7/9 = x/100
Cross-multiplying:
9x = 700
Solving for x:
x = 700/9 ≈ 77.78%
2. Using a Calculator: Most calculators possess a percentage function that simplifies the conversion. Simply enter 7 ÷ 9 and then multiply by 100. The calculator will directly display the percentage.
Applications of Percentage Calculations
The ability to calculate percentages extends far beyond simple mathematical exercises. Understanding percentages is crucial in various aspects of life:
1. Academic Performance: Grades are often expressed as percentages, representing the ratio of correct answers to total questions. Calculating your grade percentage helps you monitor your academic progress.
2. Financial Management: Percentages play a pivotal role in personal finance. Understanding interest rates, discounts, taxes, and investment returns requires a solid grasp of percentage calculations. For example, calculating the percentage increase or decrease in your savings or investments allows you to track financial growth effectively.
3. Data Analysis and Statistics: Percentages are fundamental to data representation and interpretation. They enable comparisons across different datasets and provide a standardized way to express proportions. Researchers frequently use percentages to summarize findings and draw meaningful conclusions from their data. For instance, expressing survey results as percentages facilitates easy understanding of respondent preferences or opinions.
4. Business and Commerce: Percentages are vital in business for pricing, profit margins, sales growth, market share analysis, and various other calculations. For example, determining the markup percentage on a product helps establish the selling price and ensures profitability. Analyzing sales growth percentages helps businesses track their progress and make informed strategic decisions.
5. Everyday Life: Percentages are embedded in everyday scenarios. Calculating tips at restaurants, understanding discounts at stores, interpreting sales tax rates, and comprehending nutritional information on food labels are all examples of where percentage calculations are routinely employed.
Understanding Recurring Decimals and Rounding
The calculation of 7/9 resulted in a recurring decimal (0.777...). Recurring decimals are decimals where one or more digits repeat infinitely. In practical applications, we usually round recurring decimals to a manageable number of decimal places, such as two decimal places (77.78%) for clarity and precision. The level of rounding depends on the desired accuracy of the calculation.
Expanding Your Knowledge: Related Percentage Concepts
Beyond calculating a simple percentage, understanding related concepts can further enhance your mathematical skills and proficiency in handling percentages. These concepts include:
-
Percentage Increase/Decrease: This involves calculating the change in a value as a percentage of the original value. It's crucial for understanding growth rates (e.g., population growth, economic growth) or declines (e.g., stock market losses, reduction in sales).
-
Percentage Point Difference: It's essential to distinguish between percentage points and percentages. A percentage point difference refers to the arithmetic difference between two percentages, while a percentage difference is the relative change between two percentages. For instance, a change from 10% to 15% represents a 5-percentage point increase but a 50% percentage increase.
-
Compounding Percentages: This concept is important in finance and investment, where interest or returns are calculated not only on the principal amount but also on the accumulated interest.
-
Weighted Averages: Weighted averages apply different weights to different values, which are particularly useful when dealing with datasets where not all values hold equal importance.
-
Percentage Error: This is a measure of the inaccuracy of a measurement or calculation, expressed as a percentage of the true value. It is a crucial concept for assessing the reliability of data or experimental results.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate "7 out of 9 as a percentage" is a stepping stone to mastering broader percentage-related skills. This guide has presented multiple methods for calculating percentages, highlighted their applications in various fields, and emphasized the importance of understanding recurring decimals and rounding. By grasping the fundamental principles and exploring related concepts, you can confidently tackle percentage-based problems and apply this crucial skill to numerous aspects of your personal and professional life. Remember, practice makes perfect – the more you work with percentages, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
How Many Weeks Is 10 Years
May 14, 2025
-
How Many Days Till November 25 2024
May 14, 2025
-
How Many Sticks Of Butter Is 3 Cups
May 14, 2025
-
How Many Mls Are In 8 Oz
May 14, 2025
-
How Many Square Miles Is 500 Acres
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 7 Out Of 9 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.