What Is 8 Out Of 9 As A Percentage
Webtuts
May 13, 2025 · 4 min read
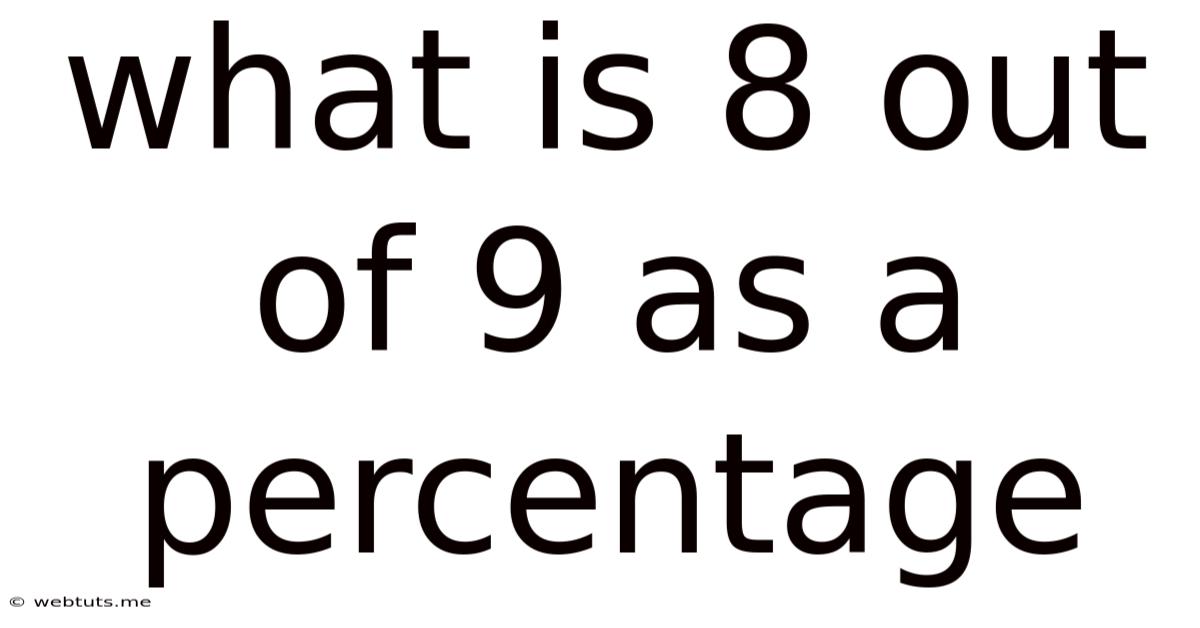
Table of Contents
What is 8 out of 9 as a Percentage? A Comprehensive Guide
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday finances to complex scientific calculations. Understanding how to express fractions as percentages allows for easier comparisons and a clearer understanding of proportions. This article will delve into the calculation of "8 out of 9 as a percentage," providing a step-by-step guide, exploring related concepts, and offering practical applications.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are widely used because they provide a standardized way to compare proportions, regardless of the overall size of the quantities involved.
Calculating 8 out of 9 as a Percentage
The question "What is 8 out of 9 as a percentage?" can be solved using a straightforward method:
Step 1: Express the fraction:
The phrase "8 out of 9" is represented as the fraction 8/9. This fraction indicates that 8 represents a part of a whole consisting of 9 equal parts.
Step 2: Convert the fraction to a decimal:
To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number). In this case:
8 ÷ 9 ≈ 0.888...
The result is a recurring decimal, meaning the digit 8 repeats infinitely. For practical purposes, we'll round this to a suitable number of decimal places.
Step 3: Convert the decimal to a percentage:
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol.
0.888... × 100 ≈ 88.89%
Therefore, 8 out of 9 is approximately 88.89%. The recurring decimal nature means that this is an approximation; the precise percentage is 88.888...% repeating infinitely.
Different Methods for Percentage Calculation
While the above method is straightforward, there are other ways to approach this calculation:
Method 1: Using Proportions
We can set up a proportion to solve this:
8/9 = x/100
To solve for 'x' (the percentage), cross-multiply:
9x = 800
x = 800/9 ≈ 88.89
This confirms our previous result.
Method 2: Using a Calculator
Most calculators have a percentage function. Simply enter 8 ÷ 9 and then multiply by 100 to obtain the percentage.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in many real-world scenarios:
Finance
- Interest Rates: Calculating interest earned on savings accounts or interest paid on loans involves percentages.
- Discounts: Determining the final price of an item after a discount is applied requires percentage calculations.
- Taxes: Calculating sales tax or income tax involves applying percentage rates to the base amount.
- Investment Returns: Tracking investment performance often involves calculating percentage changes in value.
Science and Statistics
- Data Analysis: Percentages are frequently used to represent proportions within datasets.
- Probability: Expressing the likelihood of events often involves percentages.
- Experimental Results: Presenting experimental results often involves showing percentage changes or proportions.
Everyday Life
- Tip Calculation: Calculating a tip in a restaurant involves finding a percentage of the bill total.
- Grading Systems: Many grading systems in education utilize percentages to represent student performance.
- Recipe Scaling: Adjusting recipe quantities proportionally often involves percentage calculations.
Beyond the Basics: Understanding Percentage Change
While calculating a percentage from a fraction is important, understanding percentage change is equally vital. Percentage change measures the relative difference between two values. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] × 100
For example, if a stock price increases from $50 to $60, the percentage change is:
[(60 - 50) / 50] × 100 = 20%
Advanced Percentage Calculations: Percentage Increase and Decrease
Percentage increase and decrease are specific types of percentage change. They show how much a value has grown or shrunk relative to its original value.
-
Percentage Increase: Calculated by finding the difference between the new value and the old value, dividing by the old value, and multiplying by 100. It's always a positive value if there's an increase.
-
Percentage Decrease: Calculated similarly, but the result is negative if the new value is lower than the original.
Error Analysis and Significant Figures
When working with percentages, particularly those derived from recurring decimals, it's important to consider significant figures. Rounding to an appropriate number of decimal places is crucial to avoid misleading precision. The number of significant figures should reflect the accuracy of the original data.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill that enhances problem-solving abilities across a wide range of fields. Understanding the basic principles, exploring different calculation methods, and recognizing the practical applications of percentages are key to effectively using this fundamental mathematical concept. From everyday finances to complex scientific analyses, the ability to accurately calculate and interpret percentages is an indispensable tool for informed decision-making. Remember to always consider the context and appropriate level of precision when working with percentages. By understanding these concepts thoroughly, you can confidently tackle various percentage-related problems and utilize this knowledge effectively in your personal and professional life. The ability to confidently interpret and use percentages is a highly transferable skill, making it a valuable asset in many different aspects of modern life.
Latest Posts
Latest Posts
-
How Many Pounds Is 25 Tons
May 13, 2025
-
How Many Meters Are In 30 Yards
May 13, 2025
-
How Many Cups Is 7 Pints
May 13, 2025
-
How Many Tbsp Is 1 3 Stick Of Butter
May 13, 2025
-
How Many Inches Is 130 Mm
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 8 Out Of 9 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.