What Is The Decimal For 3/10
Webtuts
May 13, 2025 · 5 min read
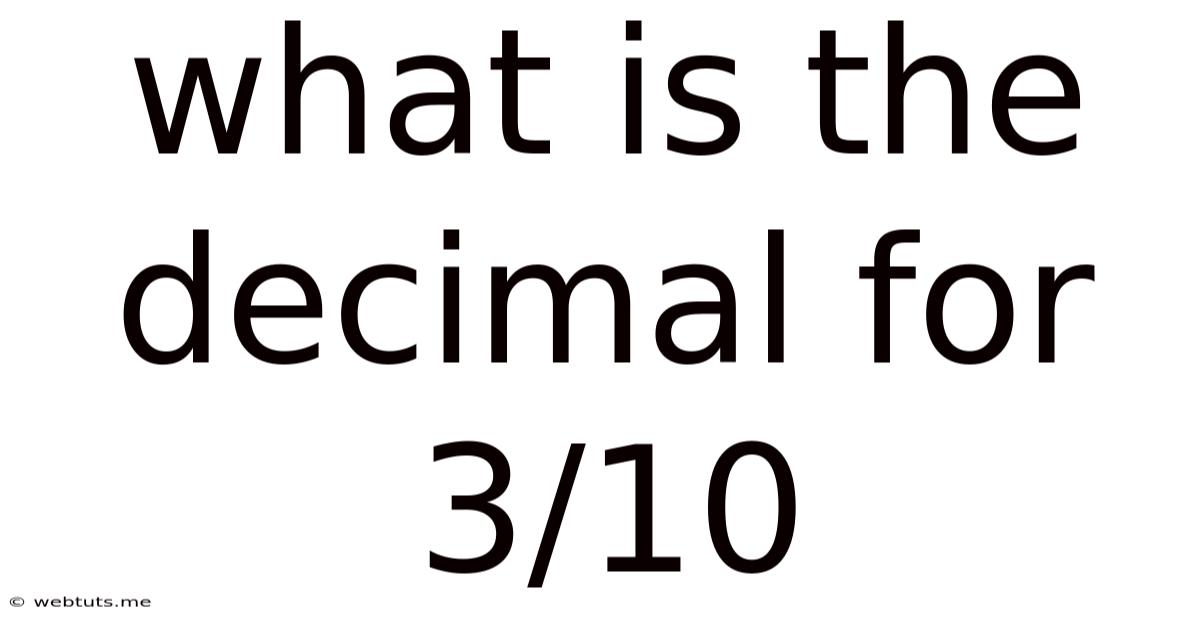
Table of Contents
What is the Decimal for 3/10? A Deep Dive into Decimal Conversion
The seemingly simple question, "What is the decimal for 3/10?", opens a door to a broader understanding of fractions, decimals, and their interrelationship within the realm of mathematics. While the answer itself is straightforward – 0.3 – the journey to understanding why this is the answer reveals fundamental concepts crucial for numeracy and problem-solving. This article will delve into this seemingly simple conversion, exploring the underlying principles and expanding upon its practical applications.
Understanding Fractions and Decimals
Before we dive into the specific conversion of 3/10, let's establish a solid foundation by defining fractions and decimals.
Fractions: Representing Parts of a Whole
A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/10, 3 is the numerator and 10 is the denominator. This means we have 3 parts out of a total of 10 equal parts.
Decimals: Another Way to Represent Parts of a Whole
Decimals are another way to represent parts of a whole. They use a base-ten system, where each digit to the right of the decimal point represents a power of ten. The first digit to the right of the decimal point represents tenths (1/10), the second represents hundredths (1/100), the third represents thousandths (1/1000), and so on.
Converting Fractions to Decimals: The Method
The conversion of a fraction to a decimal involves dividing the numerator by the denominator. This process reveals the decimal equivalent of the fraction. Let's apply this to our example: 3/10.
Step-by-Step Conversion of 3/10
-
Divide the numerator by the denominator: We divide 3 (the numerator) by 10 (the denominator).
-
Perform the division: 3 ÷ 10 = 0.3
Therefore, the decimal equivalent of 3/10 is 0.3.
Deeper Dive into the Conversion Process
The simplicity of this particular conversion masks the underlying principles that apply to more complex fraction-to-decimal conversions. Let's explore these principles:
Understanding Place Value
The decimal system relies heavily on place value. Each digit in a number holds a specific value depending on its position relative to the decimal point. In the decimal 0.3, the digit 3 occupies the tenths place, signifying 3/10.
Long Division for More Complex Fractions
While 3/10 is easily divisible, many fractions require long division to obtain their decimal equivalents. For instance, converting a fraction like 7/8 involves a more extended division process. Long division systematically breaks down the division into manageable steps, ensuring an accurate decimal representation.
Terminating and Repeating Decimals
When converting fractions to decimals, you'll encounter two types of decimal representations:
-
Terminating Decimals: These decimals have a finite number of digits after the decimal point. Our example, 0.3, is a terminating decimal.
-
Repeating Decimals (or Recurring Decimals): These decimals have a sequence of digits that repeat infinitely. For example, 1/3 converts to 0.3333..., where the digit 3 repeats indefinitely. Repeating decimals are often represented with a bar over the repeating digits (e.g., 0.3̅).
The type of decimal you obtain depends on the relationship between the numerator and the denominator of the fraction. Fractions with denominators that are powers of 10 (10, 100, 1000, etc.) will always produce terminating decimals. Fractions with denominators that have prime factors other than 2 and 5 may result in repeating decimals.
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals is vital in numerous real-world applications across various fields:
Everyday Calculations
From calculating discounts in shopping to splitting bills amongst friends, understanding decimal equivalents simplifies everyday mathematical tasks. Converting fractions to decimals allows for easier calculations and comparisons.
Measurement and Engineering
Many measurements, especially in the metric system, involve decimal values. Converting fractions to decimals is essential for accurate calculations in engineering, construction, and scientific applications.
Financial Calculations
Financial calculations, such as interest rates, stock prices, and currency conversions, rely heavily on decimal representation. Understanding fraction-to-decimal conversion is fundamental for comprehending and managing financial matters.
Data Analysis and Statistics
In data analysis and statistics, decimal values are frequently used to represent proportions, probabilities, and other statistical measures. Converting fractions to decimals facilitates data analysis and interpretation.
Computer Science and Programming
Computers work with binary numbers (base-2), but many programming languages use decimal representation for numerical data. Understanding decimal conversion is crucial for efficient data manipulation and processing.
Expanding on the Concept: Beyond 3/10
While we have focused on 3/10, the principles discussed apply to converting any fraction to a decimal. The key lies in understanding the division process, place value, and the nature of terminating and repeating decimals.
Let's consider some other examples:
- 1/4: 1 ÷ 4 = 0.25 (Terminating decimal)
- 1/3: 1 ÷ 3 = 0.333... (Repeating decimal)
- 5/8: 5 ÷ 8 = 0.625 (Terminating decimal)
- 2/7: 2 ÷ 7 = 0.285714285714... (Repeating decimal)
These examples demonstrate the versatility of the fraction-to-decimal conversion process and its applicability across a range of numerical representations.
Conclusion: Mastering Decimal Conversion
The conversion of 3/10 to 0.3, while seemingly trivial, serves as a gateway to a deeper understanding of fractions, decimals, and their practical applications. Mastering this conversion, along with the underlying principles, equips individuals with crucial numeracy skills applicable to various fields. From everyday calculations to complex scientific applications, the ability to seamlessly convert between fractions and decimals is a valuable asset in navigating the numerical world. By understanding the nuances of terminating and repeating decimals, and by mastering long division techniques, one can confidently handle any fraction-to-decimal conversion encountered. The simple question of "What is the decimal for 3/10?" thus unfolds into a comprehensive exploration of a fundamental mathematical concept.
Latest Posts
Latest Posts
-
What Is A Square Yard In Feet
May 13, 2025
-
What Is 6 Fl Oz In Cups
May 13, 2025
-
How Many Days Till The 4th
May 13, 2025
-
1m Is Equal To How Many Mm
May 13, 2025
-
2 4 Kg Is How Many Pounds
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Decimal For 3/10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.