What Is The Fraction For 0.375
Webtuts
May 14, 2025 · 4 min read
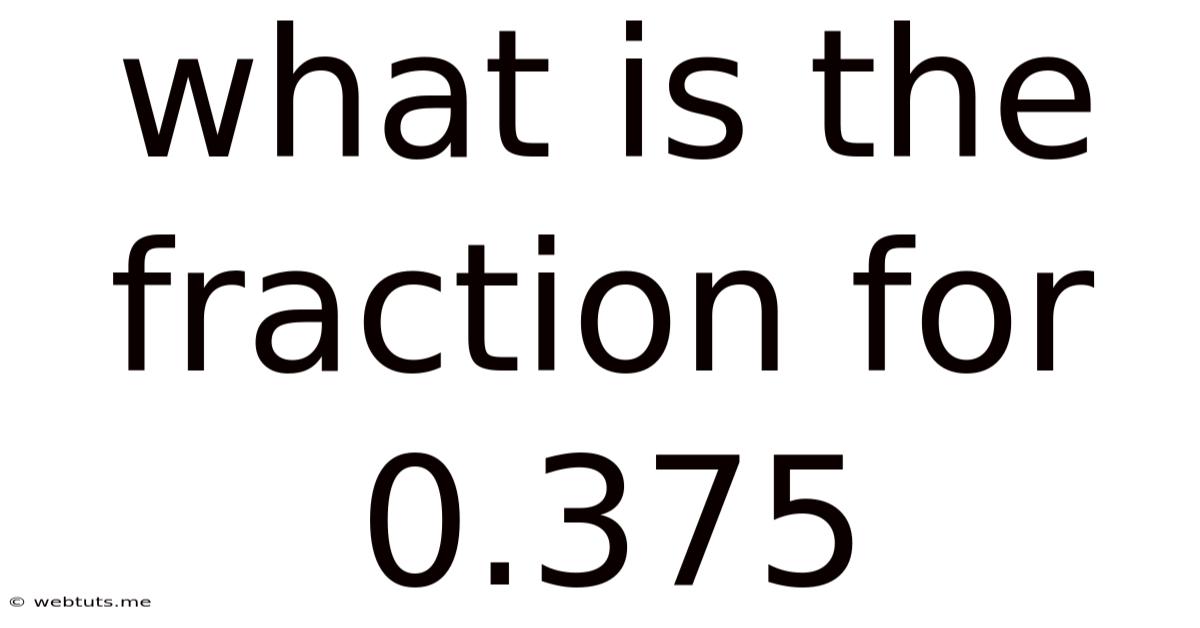
Table of Contents
What is the Fraction for 0.375? A Deep Dive into Decimal-to-Fraction Conversion
The seemingly simple question, "What is the fraction for 0.375?", opens a door to a fascinating world of mathematical concepts, particularly the conversion between decimals and fractions. While the answer itself is straightforward, understanding the why behind the conversion process is crucial for anyone seeking a solid grasp of mathematical principles. This article will not only provide the answer but delve deep into the methods and reasoning behind converting decimals to fractions, exploring various approaches and their applications.
Understanding Decimals and Fractions
Before we tackle the conversion of 0.375, let's establish a firm understanding of decimals and fractions.
Decimals: Decimals represent numbers that are not whole numbers. They use a base-ten system, with each digit to the right of the decimal point representing a decreasing power of 10. For example, 0.375 represents 3 tenths (0.3), 7 hundredths (0.07), and 5 thousandths (0.005).
Fractions: Fractions represent parts of a whole. They are expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
Converting 0.375 to a Fraction: The Step-by-Step Process
The key to converting a decimal to a fraction lies in understanding the place value of the last digit. In 0.375, the last digit, 5, is in the thousandths place. This means that 0.375 can be expressed as 375 thousandths. We can write this as a fraction:
375/1000
Now, we simplify this fraction by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Finding the GCD of 375 and 1000 can be done through several methods, including:
-
Prime Factorization: This involves breaking down both numbers into their prime factors. 375 = 3 × 5³, and 1000 = 2³ × 5³. The common factors are 5³, which equals 125.
-
Euclidean Algorithm: This is a more efficient method for larger numbers, involving repeated division until the remainder is 0.
Once we find the GCD (125 in this case), we divide both the numerator and denominator by it:
375 ÷ 125 = 3 1000 ÷ 125 = 8
This gives us the simplified fraction:
3/8
Therefore, the fraction for 0.375 is 3/8.
Alternative Methods for Decimal to Fraction Conversion
While the method outlined above is the most straightforward, other approaches can be used depending on the complexity of the decimal.
Method 2: Using Place Value Directly
For decimals with a limited number of digits after the decimal point, you can directly write the decimal as a fraction based on its place value. For instance:
- 0.3 = 3/10
- 0.07 = 7/100
- 0.005 = 5/1000
Then, add these fractions together to get the final fraction. This approach can be more cumbersome for decimals with many digits.
Method 3: Repeating Decimals
Repeating decimals, such as 0.333..., present a slightly more complex scenario. These require a different approach involving algebraic manipulation. We won't delve into this here, but it's important to note that different techniques are needed for repeating and non-repeating decimals.
Applications of Decimal-to-Fraction Conversion
The ability to convert decimals to fractions is essential in various mathematical contexts and real-world applications:
-
Baking and Cooking: Recipes often use fractional measurements, making conversion necessary when using digital scales that provide decimal measurements.
-
Engineering and Construction: Precise measurements are critical, and using fractions ensures accuracy.
-
Finance and Accounting: Dealing with percentages and proportions often necessitates converting between decimals and fractions.
-
Data Analysis: Understanding proportions and ratios within datasets requires comfortable manipulation of fractions and decimals.
Beyond 0.375: Practicing Decimal-to-Fraction Conversions
To solidify your understanding, let's practice converting other decimals to fractions:
-
0.25: This represents 25 hundredths, or 25/100. Simplifying by dividing by 25 yields 1/4.
-
0.6: This represents 6 tenths, or 6/10. Simplifying by dividing by 2 yields 3/5.
-
0.125: This represents 125 thousandths, or 125/1000. Simplifying by dividing by 125 yields 1/8.
Mastering Decimal-to-Fraction Conversion: Tips and Tricks
-
Practice regularly: Consistent practice is key to mastering any mathematical skill.
-
Understand place value: A strong grasp of place value is foundational.
-
Simplify fractions: Always simplify fractions to their lowest terms.
-
Use different methods: Experiment with various methods to find the approach that suits you best.
-
Check your work: Verify your answer by converting the fraction back to a decimal.
Conclusion: The Power of Understanding Fractions and Decimals
The simple question, "What is the fraction for 0.375?", has led us on a journey into the world of decimal-to-fraction conversion. Understanding this conversion is not merely about getting the right answer (3/8); it's about grasping the underlying mathematical principles that govern the relationship between decimals and fractions. This understanding unlocks a broader appreciation of mathematical concepts and equips you with a valuable skill applicable across various fields. By mastering this seemingly simple task, you'll build a stronger foundation for tackling more complex mathematical challenges. So, continue practicing, explore different methods, and enjoy the journey of mathematical discovery!
Latest Posts
Latest Posts
-
How Many Days Till Aug 20
May 14, 2025
-
How Many More Days Till April 7
May 14, 2025
-
How Many Days To March 10
May 14, 2025
-
2 3 Cup Convert To Tablespoons
May 14, 2025
-
How Many Ounces In A 5 Pound Bag Of Flour
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Fraction For 0.375 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.