What Is The Percent Of 7 10
Webtuts
May 11, 2025 · 5 min read
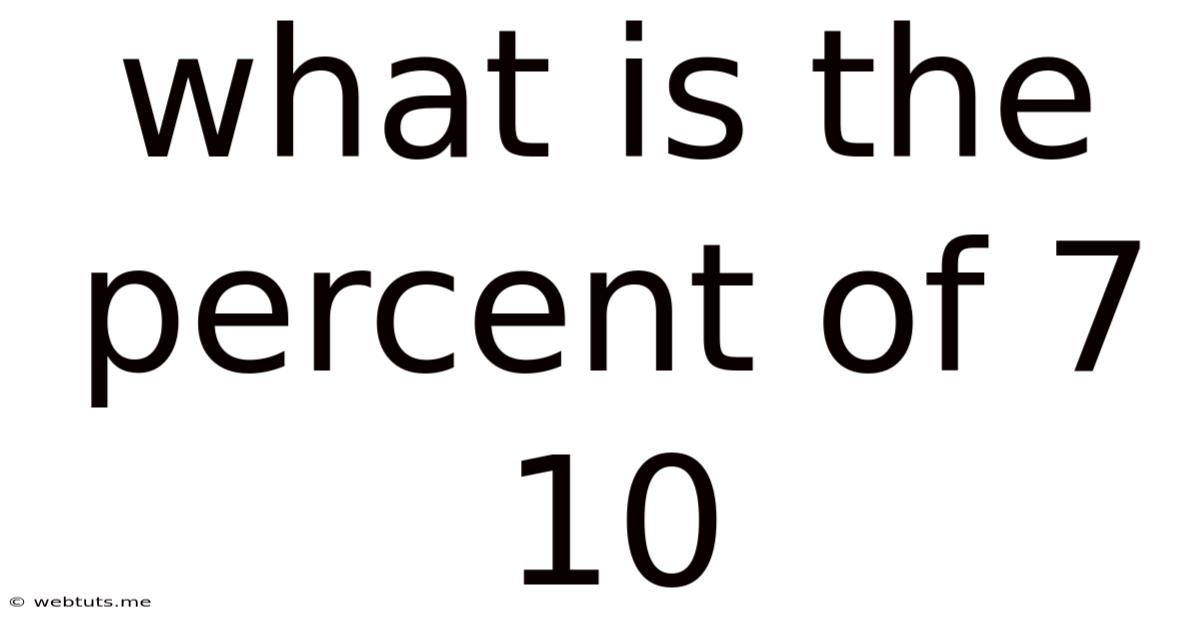
Table of Contents
What is the Percent of 7/10? A Deep Dive into Percentage Calculations and Applications
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and sales tax to comprehending financial reports and statistical data. This article explores the question, "What is the percent of 7/10?", providing a detailed explanation of the calculation process, demonstrating various approaches, and highlighting the practical uses of percentage calculations.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). Therefore, expressing a value as a percentage indicates what proportion it represents of a whole, divided into 100 equal parts.
For instance, 50% signifies 50 out of 100, which is equivalent to ½ or 0.5 in decimal form. Similarly, 25% represents 25 out of 100, equating to ¼ or 0.25. The key is understanding the relationship between fractions, decimals, and percentages—they are all different ways of representing the same proportional value.
Calculating the Percentage of 7/10
The fraction 7/10 represents seven parts out of ten. To express this as a percentage, we need to convert it to a fraction with a denominator of 100. We can achieve this through several methods:
Method 1: Direct Conversion using Proportions
We can set up a proportion:
7/10 = x/100
To solve for 'x' (the percentage), we cross-multiply:
10x = 700
x = 700/10
x = 70
Therefore, 7/10 is equivalent to 70%.
Method 2: Converting the Fraction to a Decimal
First, convert the fraction 7/10 to a decimal by dividing the numerator (7) by the denominator (10):
7 ÷ 10 = 0.7
Next, multiply the decimal by 100 to express it as a percentage:
0.7 x 100 = 70%
This confirms that 7/10 is equal to 70%.
Method 3: Using Percentage Formula
The basic percentage formula is:
Percentage = (Part/Whole) x 100
In our case:
Part = 7 Whole = 10
Therefore:
Percentage = (7/10) x 100 = 70%
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios. Let's explore some examples:
1. Financial Calculations
-
Interest Rates: Banks and financial institutions use percentages extensively to calculate interest on loans and savings accounts. Understanding percentages helps individuals manage their finances effectively.
-
Discounts and Sales Tax: Retailers use percentages to advertise discounts (e.g., "20% off") and to calculate sales tax on purchases. Consumers need to understand percentages to calculate the final price of goods.
-
Investment Returns: Investors use percentages to track the performance of their investments, assessing the rate of return on their investments.
-
Budgeting and Financial Planning: Individuals and businesses use percentages to budget their income and expenses, tracking percentages of income allocated to different categories.
2. Academic Assessments
-
Grades and Scores: Percentages are used ubiquitously in education to express student performance on tests, assignments, and overall grades.
-
Statistical Analysis: Percentages are employed to represent and interpret data in various academic fields, including research and data analysis.
3. Scientific Applications
-
Data Representation: Scientists frequently use percentages to express proportions in experiments, surveys, and research findings. This allows for clear communication and interpretation of results.
-
Concentration and Solutions: In chemistry and other scientific disciplines, percentages are used to describe the concentration of solutions. For instance, a 10% solution indicates that 10% of the solution's volume or mass is the solute.
4. Everyday Life Applications
-
Tip Calculations: Restaurant patrons use percentages to calculate appropriate tips based on the total bill.
-
Sales and Promotions: Understanding percentages helps consumers to identify and take advantage of the best deals offered by retailers.
-
Comparing Prices: Percentages assist in comparing prices of similar products from different stores, helping individuals make informed buying decisions.
-
Understanding Surveys and Polls: Many surveys and polls present data as percentages, facilitating the interpretation of public opinion or trends.
Beyond the Basics: More Complex Percentage Problems
While calculating the percentage of 7/10 is straightforward, more complex scenarios often arise. Let's consider some examples:
Example 1: Finding the Percentage Increase or Decrease
Suppose a product's price increased from $100 to $120. To calculate the percentage increase:
- Find the difference: $120 - $100 = $20
- Divide the difference by the original price: $20/$100 = 0.2
- Multiply by 100 to express as a percentage: 0.2 x 100 = 20%
Therefore, the price increased by 20%.
Similarly, a decrease can be calculated by the same method, but the final result will be negative, indicating a percentage decrease.
Example 2: Calculating Percentage of a Percentage
Consider a scenario where you receive a 10% discount on an item priced at $100, and then a further 5% discount on the discounted price. The first discount is $10 (10% of $100), leaving a price of $90. The second discount is 5% of $90, which is $4.50. The final price after both discounts is $85.50. This shows that percentages cannot always be simply added; calculating each discount sequentially is necessary.
Example 3: Calculating Percentage Change Across Multiple Periods
Imagine tracking the growth of an investment over several years. To calculate the overall percentage change, you would not simply add up the yearly percentage changes. The correct approach involves calculating the final value relative to the initial value and expressing this as a percentage.
Conclusion
The calculation of 7/10 as a percentage (70%) is a fundamental concept with far-reaching applications. Mastering percentage calculations allows individuals to navigate various situations involving proportions, ratios, and financial computations. By understanding the different methods of calculation and applying them to real-world scenarios, one can build a strong foundation in mathematical literacy and enhance their problem-solving abilities in diverse contexts. This understanding will prove invaluable in both personal and professional life, contributing to better decision-making and increased financial acumen.
Latest Posts
Latest Posts
-
How Many Cups Is 46 Ounces
May 13, 2025
-
How Many Cups Is 25 Ounces
May 13, 2025
-
60 Ml Is How Many Ounces
May 13, 2025
-
How Many Days Ago Was May 7
May 13, 2025
-
How Many Inches Is A Sq Ft
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 7 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.