What Is The Percentage Of 4 Out Of 7
Webtuts
May 14, 2025 · 5 min read
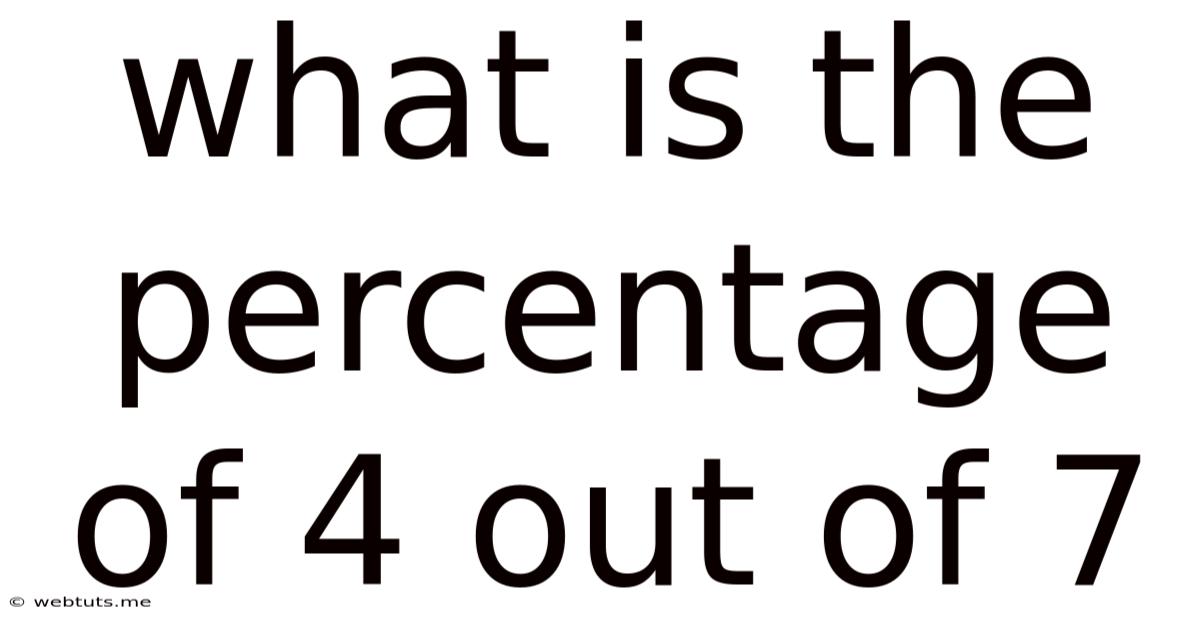
Table of Contents
What is the Percentage of 4 out of 7? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and sales tax to analyzing data and interpreting statistics. This comprehensive guide will delve into the calculation of "what is the percentage of 4 out of 7," providing not only the answer but also a thorough explanation of the underlying principles and various methods for solving similar percentage problems. We'll explore different approaches, including the use of fractions, decimals, and even simple proportion techniques. By the end of this article, you'll not only know the answer but will also possess a robust understanding of percentage calculations, empowering you to tackle a wide range of percentage-related problems.
Understanding Percentages: The Basics
Before we dive into the specific problem of calculating the percentage of 4 out of 7, let's review the fundamental concept of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," which means "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Key Terms:
- Part: This refers to the specific portion of the whole that you are interested in. In our example, the part is 4.
- Whole: This represents the total amount or the entire quantity. In our example, the whole is 7.
- Percentage: This is the numerical representation of the part relative to the whole, expressed as a percentage (%).
Method 1: Using Fractions
The most straightforward way to calculate the percentage of 4 out of 7 is by using fractions. We express the part (4) as a fraction of the whole (7):
4/7
To convert this fraction to a percentage, we need to express it as a fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by a number that will result in a denominator of 100. However, since 7 doesn't divide evenly into 100, we'll use a slightly different approach.
First, we divide the numerator (4) by the denominator (7):
4 ÷ 7 ≈ 0.5714
Next, we multiply the decimal result by 100 to convert it to a percentage:
0.5714 x 100 ≈ 57.14%
Therefore, 4 out of 7 is approximately 57.14%.
Method 2: Using Proportions
Proportions offer another effective method for solving percentage problems. A proportion is an equation that states that two ratios are equal. We can set up a proportion to solve for the percentage:
x/100 = 4/7
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
7x = 400
Now, we divide both sides by 7:
x = 400/7 ≈ 57.14
Therefore, using proportions, we arrive at the same answer: approximately 57.14%.
Method 3: Using Decimal Conversion
We can also convert the fraction 4/7 to a decimal first, and then multiply by 100 to obtain the percentage:
- Convert the fraction to a decimal: 4 ÷ 7 ≈ 0.5714
- Multiply the decimal by 100: 0.5714 x 100 ≈ 57.14%
This method yields the same result as the previous two: approximately 57.14%.
Rounding and Precision
Note that the percentage we calculated (57.14%) is an approximation. The actual decimal representation of 4/7 is a non-terminating decimal (0.571428571428...). The level of precision required depends on the context of the problem. In many cases, rounding to two decimal places (57.14%) is sufficient. However, for applications requiring higher accuracy, more decimal places may be necessary.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is essential in various real-world scenarios:
1. Business and Finance:
- Calculating profit margins: Determining the percentage of profit relative to the cost of goods sold.
- Analyzing sales data: Tracking sales growth and identifying trends.
- Calculating discounts and taxes: Applying percentage discounts or adding sales tax to the purchase price.
- Investing and returns: Assessing investment performance and calculating returns on investments.
2. Science and Statistics:
- Analyzing experimental data: Expressing results as percentages to facilitate comparisons and interpretations.
- Representing survey results: Presenting survey data in a clear and concise manner using percentages.
- Calculating probabilities: Expressing the likelihood of events occurring as percentages.
3. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in restaurants based on the bill total.
- Understanding nutritional information: Interpreting percentages of daily recommended values for nutrients in food labels.
- Comparing prices: Comparing prices of products with different sizes or quantities to determine the best value.
Beyond the Basics: More Complex Percentage Problems
While calculating the percentage of 4 out of 7 is a relatively simple problem, understanding the underlying principles allows you to tackle more complex scenarios. For example:
- Calculating percentage increase or decrease: Determining the percentage change between two values.
- Finding the original value after a percentage change: Working backwards from a percentage change to find the initial value.
- Solving problems involving multiple percentages: Calculating percentages of percentages or combining percentage changes.
Mastering the basics, as demonstrated in this guide, forms a solid foundation for tackling these more advanced percentage calculations.
Conclusion: Mastering Percentage Calculations
Calculating the percentage of 4 out of 7, as shown in this comprehensive guide, provides a practical demonstration of the fundamental principles of percentage calculations. Whether you're using fractions, proportions, or decimal conversions, the process consistently yields the same approximate result: 57.14%. Understanding the underlying concepts, along with the various methods presented here, empowers you to confidently approach a wide range of percentage problems, both simple and complex, across various disciplines and aspects of daily life. Remember that accuracy and precision depend on the context, so always consider the appropriate level of rounding when presenting your final answer. This knowledge equips you with a valuable skill set for success in academic, professional, and personal endeavors.
Latest Posts
Latest Posts
-
How Much Is 16 Oz In Liters
May 14, 2025
-
27 Gallons Is How Many Quarts
May 14, 2025
-
How Many Days Till December 10 2024
May 14, 2025
-
2 Days 12 Hours From Now
May 14, 2025
-
What Is 30 Degrees Fahrenheit In Celsius
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 4 Out Of 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.