What Percent Of 65 Is 15
Webtuts
May 10, 2025 · 4 min read
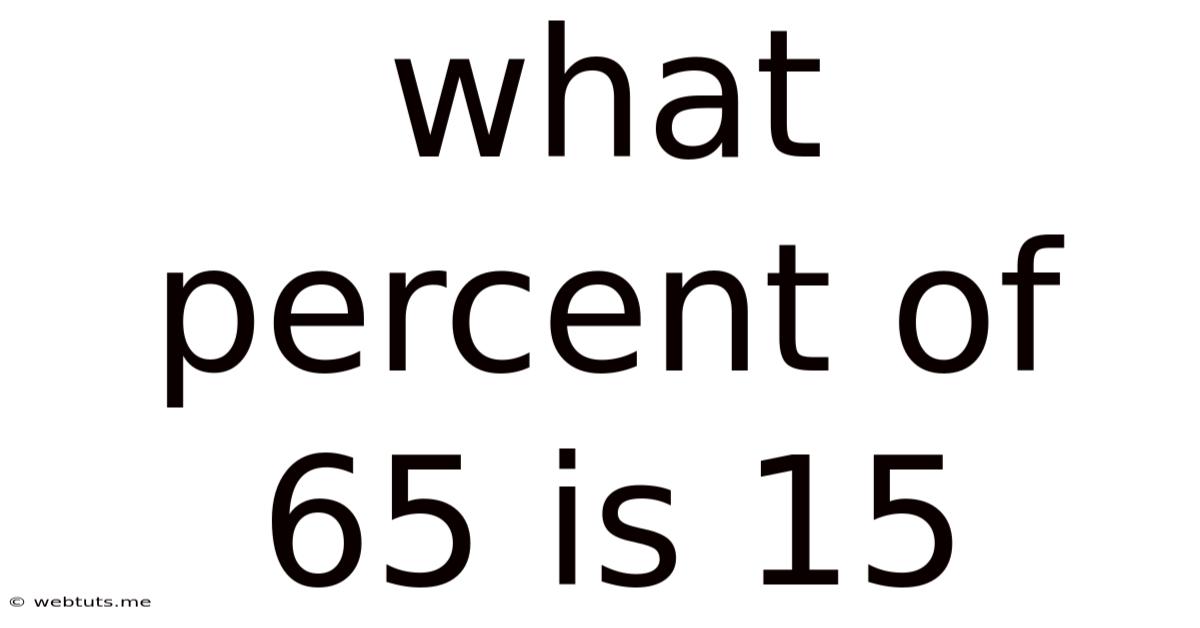
Table of Contents
What Percent of 65 is 15? A Deep Dive into Percentage Calculations
Finding what percentage one number represents of another is a fundamental mathematical skill with broad applications in everyday life, from calculating discounts and sales tax to understanding statistics and financial reports. This article explores how to determine what percent of 65 is 15, providing a step-by-step explanation, various methods for solving the problem, and practical examples to solidify your understanding. We'll also delve into the broader context of percentage calculations and their importance.
Understanding Percentages
Before tackling the specific problem, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to denote a percentage. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are incredibly useful for comparing quantities, representing proportions, and expressing changes or growth. They provide a standardized way to understand relative sizes and relationships between numbers.
Method 1: Using Proportions
One of the most straightforward methods for solving "what percent of 65 is 15?" involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as follows:
- x/100 = 15/65
Where 'x' represents the percentage we're trying to find. This equation states that the ratio of x to 100 is equal to the ratio of 15 to 65.
To solve for x, we can cross-multiply:
- 65x = 1500
Then, divide both sides by 65:
-
x = 1500 / 65
-
x ≈ 23.08%
Therefore, 15 is approximately 23.08% of 65.
Method 2: Using Decimal Conversion
Another approach involves converting the fraction 15/65 into a decimal and then multiplying by 100 to express it as a percentage.
-
Divide 15 by 65: 15 ÷ 65 ≈ 0.2308
-
Multiply by 100: 0.2308 × 100 = 23.08%
This method yields the same result as the proportion method: 15 is approximately 23.08% of 65.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process. Simply divide 15 by 65 and then multiply the result by 100. The calculator will automatically handle the conversion to a percentage. This is a quick and efficient method, especially for more complex percentage calculations.
Practical Applications
Understanding percentage calculations is crucial in many real-world scenarios:
-
Sales and Discounts: If a store offers a 20% discount on an item priced at $65, you can use percentage calculations to determine the discount amount and the final price.
-
Taxes: Calculating sales tax or income tax involves determining a percentage of a given amount.
-
Financial Analysis: Percentage changes in stock prices, investment returns, or company profits are frequently reported and analyzed.
-
Statistics: Percentages are extensively used to represent data in graphs, charts, and reports. For example, understanding survey results often requires interpreting percentages.
-
Grade Calculations: In education, grades are often expressed as percentages, representing the proportion of correct answers or points earned.
Beyond the Basics: More Complex Percentage Problems
While the problem "What percent of 65 is 15?" is relatively simple, the principles involved extend to more complex scenarios:
-
Finding the original amount: If you know a percentage and the resulting amount, you can work backward to find the original amount.
-
Calculating percentage increase or decrease: Determining the percentage change between two numbers requires understanding how to calculate the difference and express it as a percentage of the original amount.
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest, requiring iterative percentage calculations.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: Consistent practice is key to mastering percentage calculations. Try solving various percentage problems to build your confidence and speed.
-
Understand the Fundamentals: A solid grasp of fractions, decimals, and ratios is essential for understanding percentages.
-
Utilize Calculators Efficiently: Learn how to use your calculator's percentage function to save time and improve accuracy.
-
Check Your Work: Always double-check your answers to ensure accuracy, especially in high-stakes situations.
Conclusion: The Power of Percentages
The ability to calculate percentages is a valuable skill with wide-ranging applications. Understanding how to determine what percent of 65 is 15, as demonstrated through different methods in this article, is a stepping stone to mastering more complex percentage calculations. By practicing and applying these techniques, you can enhance your numerical literacy and confidently tackle percentage problems in various contexts. Remember, the seemingly simple question of "What percent of 65 is 15?" opens the door to a deeper understanding of the power and versatility of percentages in the world around us. From everyday finances to complex data analysis, the ability to work with percentages fluently is a highly valuable asset.
Latest Posts
Latest Posts
-
How Many Days Till September 13 2024
May 10, 2025
-
How Many Years Is 32 Months
May 10, 2025
-
100 Square Yard To Square Feet
May 10, 2025
-
How Many Days Since October 31
May 10, 2025
-
How Many Days Til April 9
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 65 Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.