What Percentage Is 7 Out Of 9
Webtuts
May 13, 2025 · 4 min read
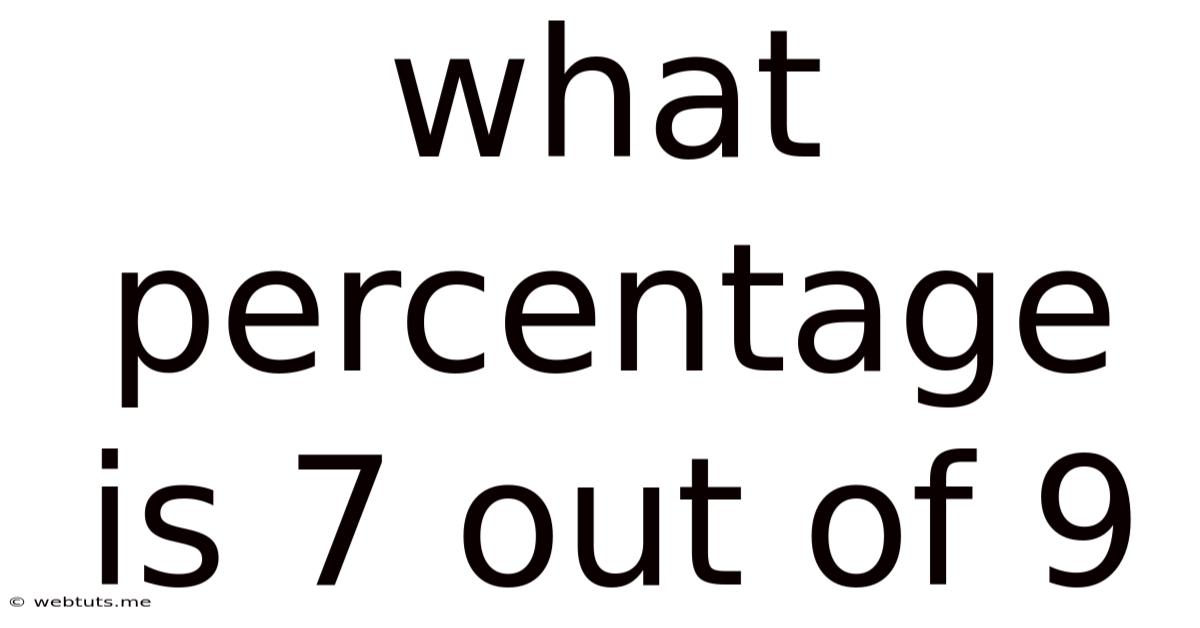
Table of Contents
What Percentage is 7 out of 9? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in numerous aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will not only answer the question, "What percentage is 7 out of 9?", but also equip you with the knowledge and tools to tackle any percentage calculation with confidence. We'll explore various methods, delve into the underlying concepts, and provide practical examples to solidify your understanding.
Calculating the Percentage: The Basic Approach
The most straightforward way to determine what percentage 7 out of 9 represents is through a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
(7 / 9) * 100% = 77.78% (approximately)
Therefore, 7 out of 9 is approximately 77.78%. The slight rounding is due to the repeating decimal nature of the result (0.7777...).
Understanding the Components
Before we delve deeper, let's clarify the terms involved:
- Part: This represents the specific portion of the whole you are interested in. In our example, the part is 7.
- Whole: This refers to the total amount or the complete unit. In our example, the whole is 9.
- Percentage: This expresses the part as a fraction of the whole, represented as a number out of 100.
Alternative Methods for Calculation
While the basic formula is efficient, other approaches can offer valuable insights and are useful for different contexts:
Method 2: Using Decimal Conversion
- Divide the part by the whole: 7 / 9 = 0.777...
- Multiply the decimal by 100%: 0.777... * 100% = 77.78% (approximately)
This method emphasizes the relationship between decimals and percentages. Understanding this connection is crucial for various mathematical applications.
Method 3: Proportion Method
This method involves setting up a proportion:
7/9 = x/100
Solving for 'x' gives you the percentage:
9x = 700 x = 700/9 x ≈ 77.78
This approach is particularly useful for visualizing the relationship between the parts and the whole in a proportional context.
Practical Applications: Real-World Examples
Let's explore some real-world scenarios where understanding this percentage calculation is invaluable:
Example 1: Test Scores
Imagine a student scored 7 out of 9 on a quiz. Using our calculation, we know they achieved approximately 77.78%. This allows for easy comparison with other scores and assessment of performance.
Example 2: Sales Conversions
A salesperson made 7 successful sales out of 9 leads contacted. This translates to a 77.78% conversion rate, providing valuable insights into sales effectiveness.
Example 3: Project Completion
A project consisting of 9 tasks has 7 completed tasks. The project completion rate is 77.78%, allowing for easy monitoring of progress.
Example 4: Survey Results
Out of 9 respondents to a survey, 7 answered "yes" to a specific question. This represents a 77.78% positive response rate, providing insights into public opinion.
Expanding Your Percentage Skills: Handling More Complex Scenarios
While the 7 out of 9 example is straightforward, many percentage problems involve more complex calculations. Here are some scenarios and approaches:
Scenario 1: Percentage Increase/Decrease
Calculating percentage changes requires a slightly different approach. For example, if a value increases from 9 to 16, the percentage increase is calculated as follows:
((16 - 9) / 9) * 100% = 77.78%
Scenario 2: Finding the Whole Given a Percentage and Part
If you know that 77.78% of a number is 7, you can find the whole number using the following formula:
(Part / Percentage) * 100 = Whole
(7 / 77.78%) * 100 = 9
Scenario 3: Multiple Percentage Calculations
When dealing with multiple percentages, it's essential to perform calculations sequentially. For instance, applying a 10% discount followed by a 5% tax requires separate calculations.
Advanced Techniques and Tools
For more complex percentage calculations involving multiple variables or large datasets, spreadsheets (like Microsoft Excel or Google Sheets) and statistical software packages can be incredibly helpful. These tools offer built-in functions for percentage calculations, significantly streamlining the process and reducing the risk of errors.
Conclusion: Mastering Percentage Calculations
Understanding percentage calculations is a critical skill applicable across diverse fields. This guide has demonstrated the fundamental methods for calculating percentages, illustrated the process with real-world examples, and expanded upon more complex scenarios. By mastering these techniques, you'll be better equipped to interpret data, make informed decisions, and effectively communicate quantitative information. Remember that consistent practice is key to building proficiency in this essential area of mathematics. Continue exploring different problems and applying these methods to solidify your understanding and confidently tackle any percentage calculation you encounter.
Latest Posts
Latest Posts
-
How Many Days Till Jan 4 2025
May 13, 2025
-
How Many Gallons In 24 Pints
May 13, 2025
-
How Many Days Are In 22 Weeks
May 13, 2025
-
How Many Weeks Until June 12th
May 13, 2025
-
How Many Days Until October 1 2025
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 7 Out Of 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.