Write 3 19 100 As A Decimal.
Webtuts
May 10, 2025 · 5 min read
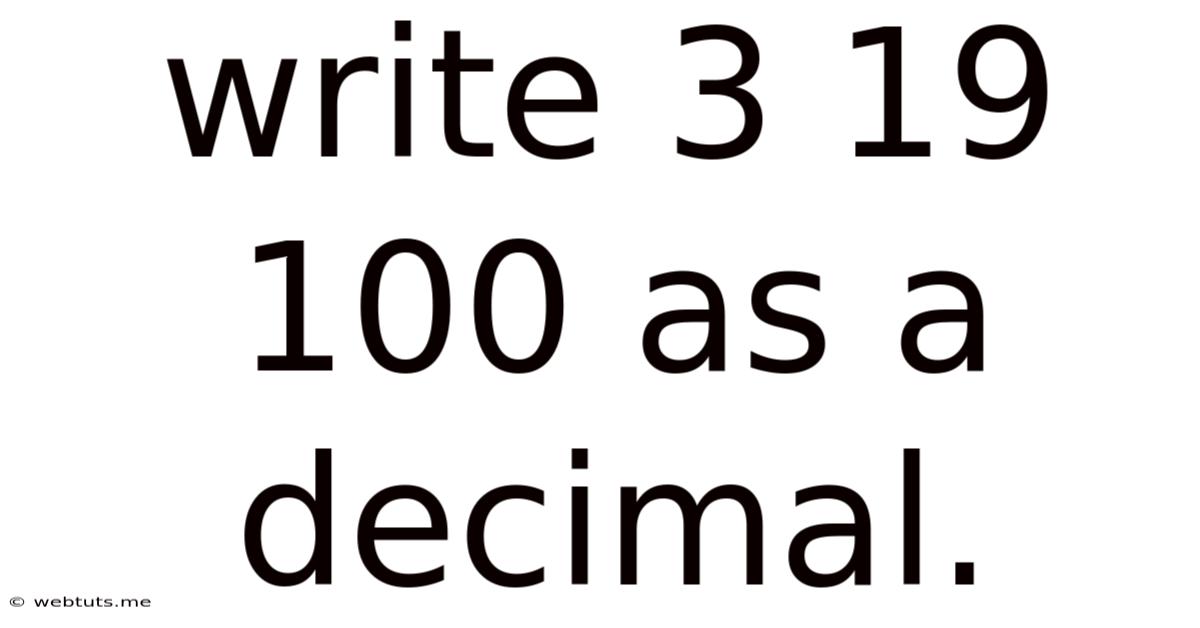
Table of Contents
Writing 3 19 100 as a Decimal: A Comprehensive Guide
Understanding how to convert mixed numbers, like 3 19/100, into decimals is a fundamental skill in mathematics. This seemingly simple task underlies many complex calculations and is crucial for various applications, from everyday finances to advanced scientific computations. This comprehensive guide will walk you through the process, explaining the underlying concepts and offering practical examples to solidify your understanding. We'll explore different methods, address common pitfalls, and delve into the broader context of decimal representation.
Understanding the Components: Whole Numbers and Fractions
Before diving into the conversion process, let's refresh our understanding of the components of a mixed number like 3 19/100. This number combines a whole number (3) and a fraction (19/100).
-
The Whole Number: This represents a complete unit, or a number of complete units. In our example, it's 3.
-
The Fraction: This represents a part of a whole unit. The numerator (19) indicates the number of parts we have, and the denominator (100) indicates the total number of equal parts the whole unit is divided into.
The key to converting a mixed number to a decimal lies in understanding that the fraction represents a portion of 1. To express this portion as a decimal, we need to divide the numerator by the denominator.
Method 1: Direct Division
The most straightforward method for converting 3 19/100 to a decimal is through direct division. This method involves dividing the numerator (19) by the denominator (100).
-
Perform the division: 19 ÷ 100 = 0.19
-
Combine with the whole number: Add the whole number (3) to the result obtained from the division. 3 + 0.19 = 3.19
Therefore, 3 19/100 written as a decimal is 3.19.
This method is particularly useful when dealing with fractions where the denominator is not a power of 10 (e.g., 10, 100, 1000, etc.). However, for fractions with denominators that are powers of 10, there's a simpler and often faster approach.
Method 2: Utilizing Place Value (for denominators that are powers of 10)
When the denominator of the fraction is a power of 10 (like 100 in our example), a faster method leverages the decimal place value system.
-
Understand place value: Recall that the decimal point separates the whole number part from the fractional part. To the right of the decimal point, the first place is the tenths place (1/10), the second place is the hundredths place (1/100), the third place is the thousandths place (1/1000), and so on.
-
Position the numerator: Since our denominator is 100 (hundredths), we place the numerator (19) in the hundredths place. This means the digits "19" will go to the right of the decimal point.
-
Combine with the whole number: We have 3 as the whole number, so we write it to the left of the decimal point.
Combining these steps, we get 3.19. This method is visually intuitive and efficient when the denominator is a power of 10.
Understanding Decimal Representation: A Deeper Dive
The decimal system is a base-10 positional numeral system. Each digit's position relative to the decimal point determines its value. For instance, in the number 3.19:
- 3: Represents three units (3 x 1)
- 1: Represents one tenth (1 x 0.1 or 1/10)
- 9: Represents nine hundredths (9 x 0.01 or 9/100)
The decimal representation provides a concise way to express both whole numbers and fractional parts of a number. This system is widely used due to its simplicity and efficiency in representing a wide range of values.
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals is crucial in various real-world scenarios:
-
Finance: Calculating percentages, interest rates, discounts, and tax amounts often requires converting fractions to decimals.
-
Measurements: Many measurements, such as lengths, weights, and volumes, are expressed using decimal notation. Converting fractional measurements to decimals simplifies calculations and comparisons.
-
Science: Scientific calculations, particularly in physics, chemistry, and engineering, heavily rely on decimal representation for accuracy and precision.
-
Data Analysis: Converting data from fractional form to decimal form is often necessary for data analysis and statistical calculations. Spreadsheet software and statistical packages typically use decimal representation.
-
Everyday Life: From calculating tips at restaurants to determining unit prices, decimal conversions are part of our daily lives.
Common Pitfalls and How to Avoid Them
While converting 3 19/100 to a decimal is relatively straightforward, some common mistakes should be avoided:
-
Misunderstanding Place Value: Incorrectly placing the digits after the decimal point can lead to errors. Always double-check that the digits align with the correct place values.
-
Incorrect Division: Make sure to perform the division (numerator divided by denominator) accurately. Use a calculator if needed, but double-check your work.
-
Forgetting the Whole Number: Don't forget to add the whole number part of the mixed number to the decimal equivalent of the fraction.
-
Decimal Point Placement: Ensuring accurate placement of the decimal point is essential for correct representation of the number.
Expanding the Concept: Converting Other Fractions to Decimals
The methods discussed above can be extended to convert other fractions to decimals. For example:
-
Fractions with denominators that are not powers of 10: Use the direct division method (numerator ÷ denominator). The result might be a terminating decimal (e.g., 1/4 = 0.25) or a repeating decimal (e.g., 1/3 = 0.333...).
-
Improper Fractions: First, convert the improper fraction into a mixed number, then follow the methods described above to convert to a decimal.
-
Complex Fractions: Simplify the complex fraction to a simpler fraction, then convert to a decimal using the appropriate method.
Conclusion: Mastering Decimal Conversions
Converting 3 19/100 to a decimal, and more generally, mastering fraction-to-decimal conversions, is an essential mathematical skill. This ability simplifies calculations, enhances understanding of numerical relationships, and is widely applicable in various fields. By understanding the underlying principles of place value, direct division, and the nature of decimal representation, you can confidently tackle these conversions and unlock a deeper understanding of numbers. Remember to practice regularly and carefully check your work to avoid common errors. The more you practice, the more fluent you'll become in navigating the world of decimals and fractions.
Latest Posts
Latest Posts
-
Find The Midpoint Of The Segment With The Following Endpoints
May 11, 2025
-
56 Quarts Is How Many Gallons
May 11, 2025
-
What Is 3 4 Pound In Ounces
May 11, 2025
-
How Many Cups Are 64 Oz
May 11, 2025
-
How Many Ounces In 17 Pounds
May 11, 2025
Related Post
Thank you for visiting our website which covers about Write 3 19 100 As A Decimal. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.