What Is 25 Off Of $40
Webtuts
May 09, 2025 · 5 min read
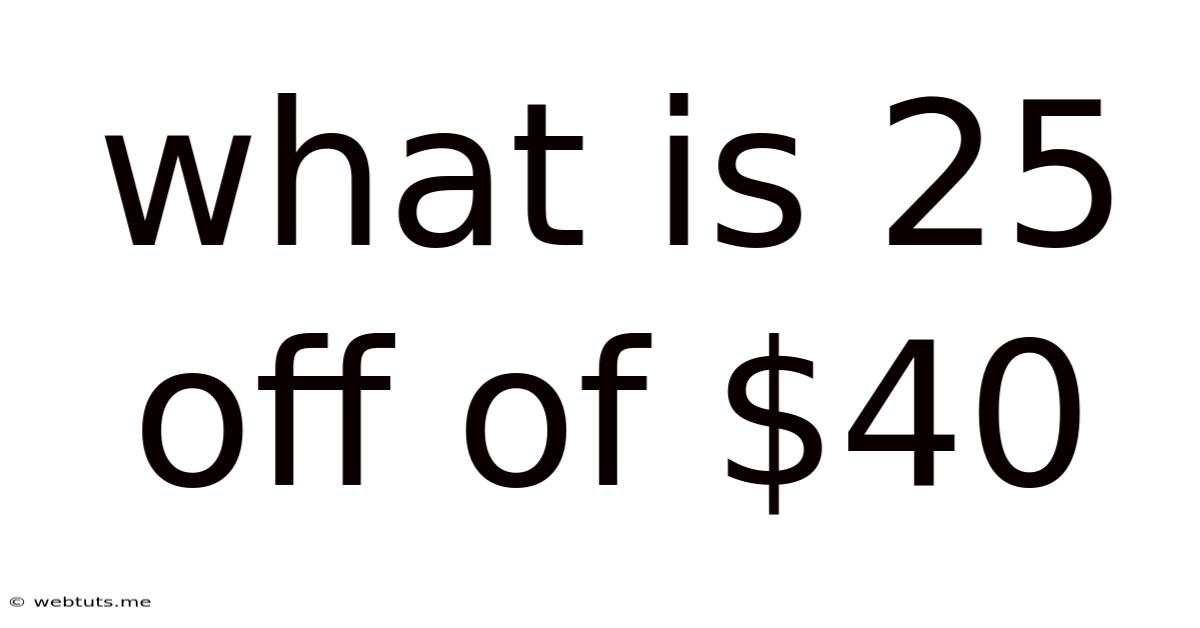
Table of Contents
What is 25% Off of $40? A Comprehensive Guide to Percentage Discounts
Calculating discounts is a crucial skill in everyday life, whether you're shopping for groceries, electronics, or planning a vacation. Understanding how to quickly and accurately determine the final price after a percentage discount can save you time and money. This article will delve into the calculation of a 25% discount on $40, explaining the process step-by-step and providing you with valuable insights into percentage calculations. We'll also explore different methods for solving this problem, equipping you with the knowledge to tackle similar discount scenarios with ease.
Understanding Percentage Discounts
Before diving into the specific calculation, let's clarify what a percentage discount represents. A percentage discount is a reduction in the original price of an item, expressed as a percentage of that original price. In our case, we have a 25% discount on a $40 item. This means the price will be reduced by 25% of $40.
Key Terms:
- Original Price: The initial price of the item before any discount is applied. In this case, the original price is $40.
- Discount Percentage: The percentage by which the original price is reduced. Here, the discount percentage is 25%.
- Discount Amount: The actual monetary value of the reduction. This is what we need to calculate.
- Final Price: The price after the discount has been applied. This is also a key value we'll determine.
Method 1: Calculating the Discount Amount Directly
This method involves calculating the discount amount first and then subtracting it from the original price to find the final price.
Step 1: Convert the Percentage to a Decimal
To work with percentages in calculations, we need to convert them to their decimal equivalents. To do this, divide the percentage by 100:
25% ÷ 100 = 0.25
Step 2: Calculate the Discount Amount
Multiply the original price by the decimal equivalent of the percentage discount:
$40 x 0.25 = $10
This means the discount amount is $10.
Step 3: Calculate the Final Price
Subtract the discount amount from the original price:
$40 - $10 = $30
Therefore, the final price after a 25% discount on $40 is $\boxed{$30}$.
Method 2: Calculating the Final Price Directly
This method involves calculating the final price directly by finding the percentage remaining after the discount and multiplying it by the original price.
Step 1: Determine the Percentage Remaining
If you're receiving a 25% discount, this means you'll pay 100% - 25% = 75% of the original price.
Step 2: Convert the Remaining Percentage to a Decimal
Convert 75% to its decimal equivalent:
75% ÷ 100 = 0.75
Step 3: Calculate the Final Price
Multiply the original price by the decimal equivalent of the remaining percentage:
$40 x 0.75 = $30
This directly gives us the final price of $\boxed{$30}$.
Comparing the Two Methods
Both methods yield the same result: a final price of $30. The first method is more intuitive for some, clearly showing the discount amount separately. The second method is often faster and more efficient, especially for more complex calculations. Choose the method that you find most comfortable and easy to understand.
Practical Applications and Real-World Scenarios
Understanding percentage discounts is essential for various real-world scenarios:
Shopping:
- Sales and promotions: Stores frequently offer percentage discounts on various items. Being able to quickly calculate the final price allows for informed purchasing decisions.
- Comparing prices: When comparing prices between different stores or online retailers, you can easily compare discounts and determine the best deal.
Budgeting and Finance:
- Calculating savings: Tracking savings from discounts helps in managing personal finances effectively.
- Understanding interest rates: Interest rates on loans and investments are expressed as percentages. Understanding percentage calculations helps in comprehending financial terms and making informed choices.
Other Applications:
- Tip calculations: Calculating tips in restaurants is a common application of percentage calculations.
- Sales commissions: Sales representatives often earn commissions based on a percentage of their sales.
- Tax calculations: Sales tax and other taxes are often calculated as a percentage of the purchase price.
Advanced Percentage Calculations: Handling Multiple Discounts
Sometimes, you might encounter situations with multiple discounts applied successively. For example, you might have a 25% discount followed by an additional 10% discount. In such cases, it's crucial to calculate the discounts sequentially. You cannot simply add the percentages together (25% + 10% = 35%) because the second discount is applied to the already reduced price.
Let's illustrate this with an example:
Original Price: $40 Discount 1: 25% Discount 2: 10%
Step 1: Apply the first discount (25%):
$40 x 0.75 = $30
Step 2: Apply the second discount (10%) to the reduced price:
$30 x 0.90 = $27
The final price after both discounts is $27. This highlights the importance of applying discounts sequentially and not simply adding the percentages.
Conclusion: Mastering Percentage Discounts
Calculating percentage discounts is a fundamental mathematical skill with numerous practical applications. Whether you're shopping for groceries, managing your finances, or navigating various aspects of your daily life, understanding how to calculate discounts effectively will empower you to make informed decisions and optimize your resources. By mastering the methods outlined in this article, you'll be well-equipped to handle a wide range of percentage-based calculations with confidence. Remember to always carefully consider the context and apply the appropriate methods to ensure accurate results, particularly when dealing with multiple discounts or complex scenarios. Practice makes perfect, so keep applying these techniques in your daily life to build your proficiency and save money along the way.
Latest Posts
Latest Posts
-
How Many More Hours Until 7 Am
May 09, 2025
-
How Many Feet Is 250 Yards
May 09, 2025
-
60 Days From June 6 2024
May 09, 2025
-
15 Out Of 16 As A Percentage
May 09, 2025
-
What Time Was Nine Hours Ago
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Off Of $40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.